平面任意力系的简化VIP免费

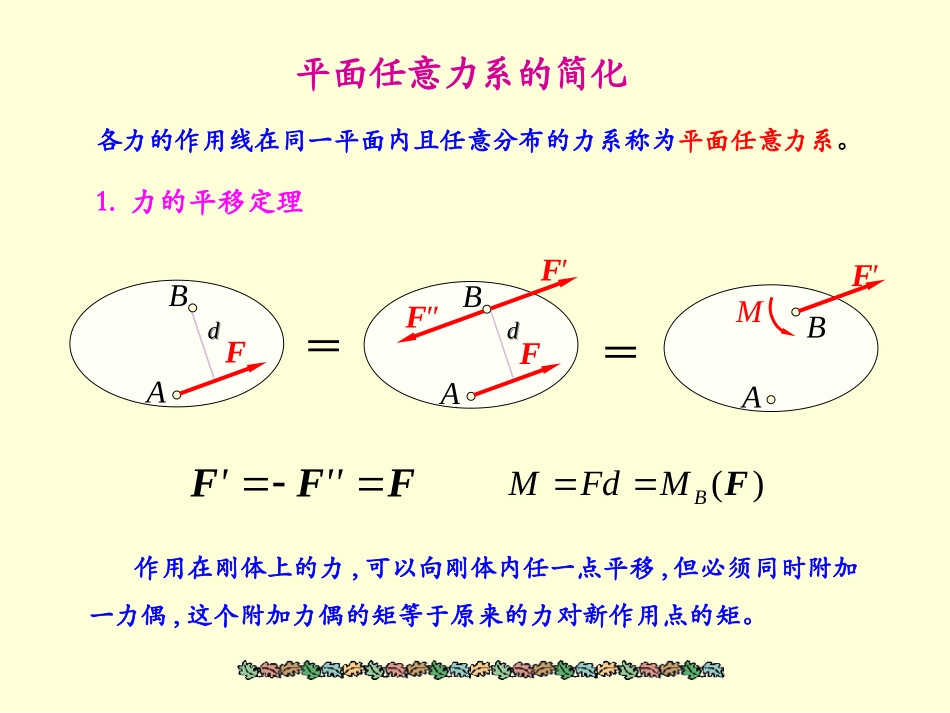
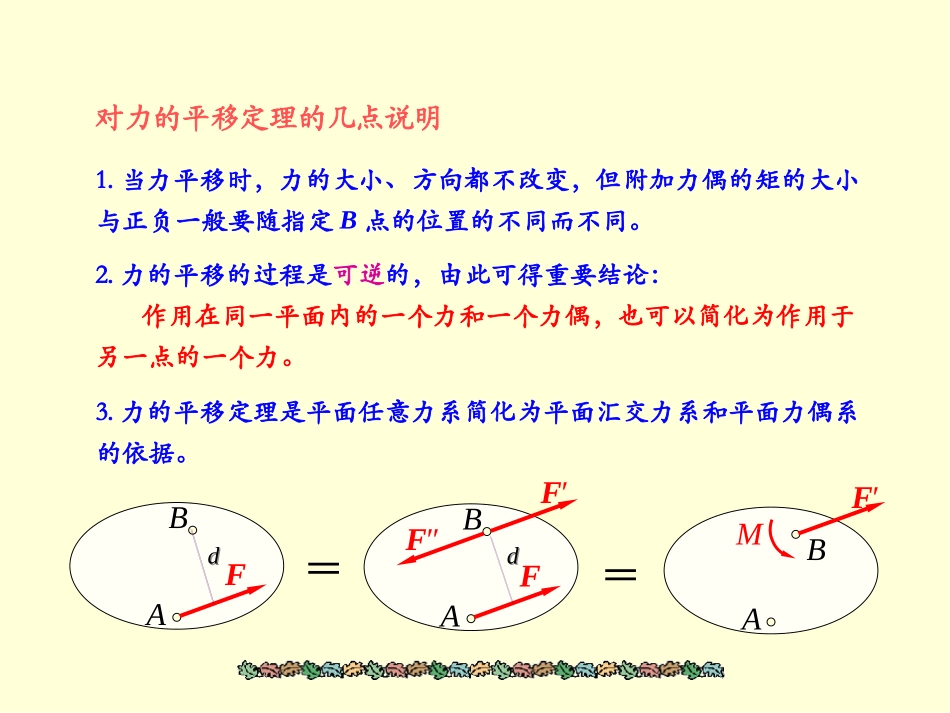
平面任意力系的简化1.力的平移定理2.平面任意力系向作用面内一点简化·主矢与主矩3.平面任意力系的简化结果分析1.力的平移定理作用在刚体上的力,可以向刚体内任一点平移,但必须同时附加一力偶,这个附加力偶的矩等于原来的力对新作用点的矩。'''FFF()BMFdMF平面任意力系的简化各力的作用线在同一平面内且任意分布的力系称为平面任意力系。ABMABF′F′F″FABF＝＝dddd对力的平移定理的几点说明1.当力平移时，力的大小、方向都不改变，但附加力偶的矩的大小与正负一般要随指定B点的位置的不同而不同。2.力的平移的过程是可逆的，由此可得重要结论：作用在同一平面内的一个力和一个力偶，也可以简化为作用于另一点的一个力。3.力的平移定理是平面任意力系简化为平面汇交力系和平面力偶系的依据。ABMABF′F′F″FABF＝＝ddddOxyijOOxyF1F2FnF1′F2′Fn′MnM2M1MOFR′2.平面任意力系向作用面内一点简化·主矢与主矩简化中心简化中心11FF22FFnnFF11()OMMF22()OMMF()nOnMMFR1212nniF'F'F'F'FFFF平面汇交力系可以合成为一个作用于点O的力，用矢量表示为称为原力系的主矢，主矢与简化中心的选择无关。1212()()()()OnOOOnOiMMMMMMMMFFFF附加力偶系可以合成为一个力偶，其力偶矩为称为原力系对简化中心O的主矩，主矩与简化中心的选择有关。平面任意力系平面汇交力系+平面力偶系向一点简化结论：平面任意力系向作用面内任一点O简化，可得一个力和一个力偶，这个力等于该力系的主矢，作用线通过简化中心O；这力偶的矩等于该力系对简化中心O的主矩。主矢与简化中心位置无关，而主矩一般与简化中心位置有关。主矢的解析表达式为RRRxyxy'''FFFF+Fij主矢FR'的大小及方向余弦为RRcos(,)xF'FFi22R()()xyFFFRRcos(,)yF'FFj主矩的大小为()OOiMMF固定端约束一物体的一端完全固定在另一物体上，这种约束称为固定端约束。实例分析AAAMAFAyFAxFAMA几点说明①认为Fi这群力在同一平面内；②将Fi向A点简化得一力和一力偶；③FA方向不定，可用正交分力FAx,FAy表示；④FAx，FAy，MA为固定端约束反力；⑤FAx,FAy限制物体平动，MA限制物体转动。A1.平面任意力系简化为一个力偶的情形如果力系的主矢等于零，而主矩不等于零，即F'R=0，MO≠0则原力系合成为合力偶。合力偶矩为MO=∑MO(Fi)根据力偶的性质（力偶矩与矩心的选择无关），易知，此时主矩与简化中心选择无关。2.平面任意力系简化为一个合力的情形·合力矩定理(1)如果力系的主矢不等于零，而主矩等于零，即F'R≠0，MO=0此时，简化中心恰好选在力系合力的作用线上，显然，F'R就是原力系的合力。3.平面任意力系的简化结果分析OO′FR′dFR″FRFRMOFR′OO′dOO′'ORMdF(2)如果力系的主矢和主矩都不等于零，即F'R≠0，MO≠0此时，原力系可进一步简化成只剩下作用于O'点的一个力，该力称为原力系的合力。如图所示合力FR的作用线到简化中心O的距离d为RRR'''FFFOO′FR′dFR″FRFRMOFR′OO′dOO′从图中可以看出()ORROMdMFF()OOiMMF由主矩的定义知所以()()OROiMMFF平面任意力系的合力对作用面内任一点的矩，等于力系中各力对同一点的矩的代数和。这就是平面任意力系的合力矩定理。3.平面任意力系平衡的情形如果力系的主矢和主矩都等于零，即F'R=0，MO=0则原力系是平衡力系，物体在该力系作用下处于平衡状态。6341P2P3PABC【例1】图示力系，已知：P1=100N,P2=50N,P3=200N,图中距离单位：cm。求：1、力系主矢及对A点之矩？2、力系简化最后结果。解：1、建立如图坐标系xy∴主矢∴=36.9°RRR200coscos(,)0.8250xF''FFi2222R()()200150250RxRyFF'F'N3200RxxF'FPN1210050150RyyF'FPPN2()6506300AAiMMPNcmFRF1P2P3PABCxy2、简化最终结果MAd主矢主矩最终结果合力大小：方向:=36.9°位置图示：方向：=36.9°在在AA点左还是右？点左还是右？R250FN300AMNcmRR250FFNRFRFR3001.2250AMdcmF【例2】在长方形平板的O，A...