变量间的相关关系VIP免费

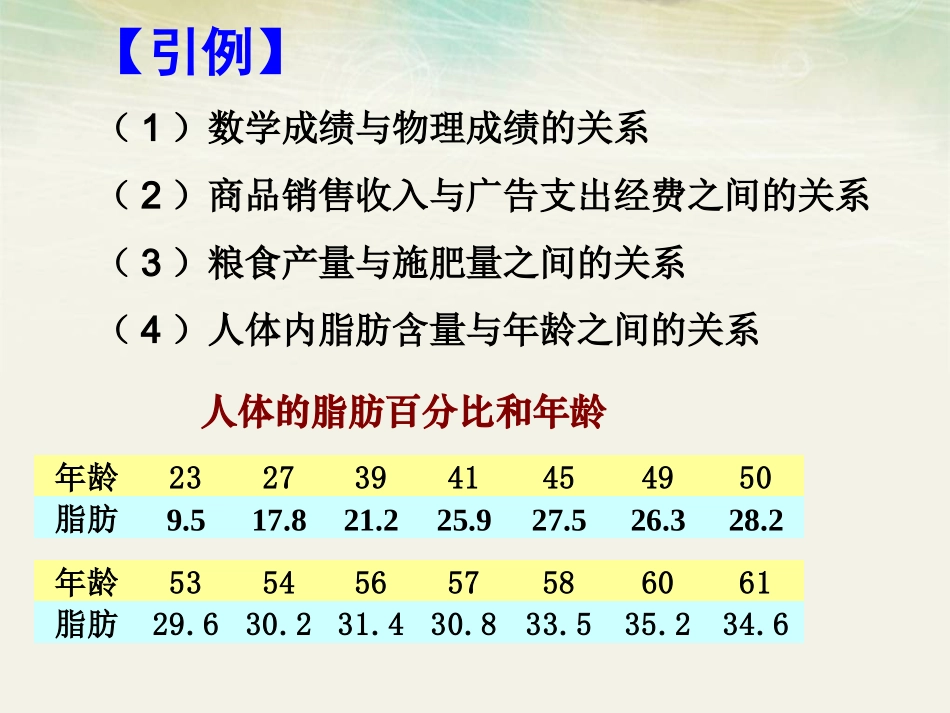
2.3两个变量的线性相关【引例】（1）数学成绩与物理成绩的关系（2）商品销售收入与广告支出经费之间的关系（3）粮食产量与施肥量之间的关系（4）人体内脂肪含量与年龄之间的关系人体的脂肪百分比和年龄年龄23273941454950脂肪9.517.821.225.927.526.328.2年龄53545657586061脂肪29.630.231.430.833.535.234.6（1）函数关系：当自变量取值一定时，因变量取值由它唯一确定1.两变量之间的关系（2）相关关系：当自变量取值一定时，因变量的取值带有一定的随机性确定关系不确定关系一、变量之间的相关关系相同点：均是指两个变量的关系不同点：函数关系是一种确定的关系;而相关关系是一种非确定关系.相关关系和函数关系的区别人体的脂肪百分比和年龄年龄23273941454950脂肪9.517.821.225.927.526.328.2年龄53545657586061脂肪29.630.231.430.833.535.234.6根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?二、两个变量的线性相关散点图：将变量所对应的点描出来，这些点组成的图就叫“散点图”“散点图”正相关：点散布在从左下角到右上角的区域.负相关：点散布在左上角到右下角的区域.O施化肥量x15202530354045水稻产量y330345365405445450455y水稻产量x(施化肥量)1020304050300350400450500【例】在7块并排、形状大小相同的试验田上进行施化肥量对水稻产量影响的试验，得到如下表所示的一组数据（单位：kg）：三、回归直线20253035404550556065年龄脂肪含量0510152025303540思考：当人的年龄增加时，体内脂肪含量到底是以什么方式增加的呢？如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.回归直线所在方程的斜率与截距的一般公式:1122211()()ˆ,()ˆˆ.nniiiiiinniiiixxyyxynxybxxxnxaybxaxbyˆˆˆ回归方程为：2221122ˆˆˆˆˆˆ()()()nnQybxaybxaybxa通过求的最小值而得出回归方程的方法，即求回归直线，使得样本数据的点到它的距离的平方和最小，这种方法叫做最小二乘法.【例1】假设关于某设备的使用年限x和所支出的维修费用y（万元）有如下的统计资料：使用年限x23456维修费用y2.23.85.56.57.0若资料知y对x呈线性相关关系，试求：1、线性回归方程y＝bx＋a的回归系数a，b。2、估计使用年限为10年时，维修费用是多少？xyxi23456yi2.23.85.56.57.0xiyi4.411.422.032.542.0xi2491625364x5y52190iix51112.3iiixy解：（1）列表如下：1221ˆ1.23niiiniixynxybxnxˆˆ0.08aybxˆ1.230.08yx（2）当x=10时，ˆ1.23100.08=12.38y万元即估计使用10年时维修费用是12.38万元.求回归方程的一般方法：1、列表2、计算,x,y,12niixiniiyx13、求,4、代入回归直线方程aˆbˆ【例2】有一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的对比表：摄氏温度-504712151923273136热饮杯数156150132128130116104899376541.画出散点图；2.从散点图中发现气温与热饮销售杯数之间的一般规律；3.求回归直线；4.如果某天的气温是2℃，预测这天卖出的热饮杯数.(2)气温与热饮杯数成负相关,即气温越高，卖出去的热饮杯数越少.(1)散点图如下：(4)当x=2时，y=143.063,因此,这天大约可以卖出143杯热饮.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（吨）与相应的生产能耗（吨标准煤）的几组对照数据．34562.5344.5y07年广东理科第17题x（1）请画出上表数据的散点图；xy（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；ybxa（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？应用实践（2）4.5,3.5,xy93.50.70.352a所以线性回归方程为ˆ0.70.35yx0.70.3570.35yx所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤．（1）266.544.53.566.5630.758644.5b（3）当x=100时，课堂小结1、两种相关关系：正相关、负相关2、回归直线所在方程的斜率与截距的一般公式:1122211()()ˆ,()ˆˆ.nniiiiiinniiiixxyyxynxybxxxnxaybxˆˆˆybxaaxbyˆˆˆ线性回归方程为：