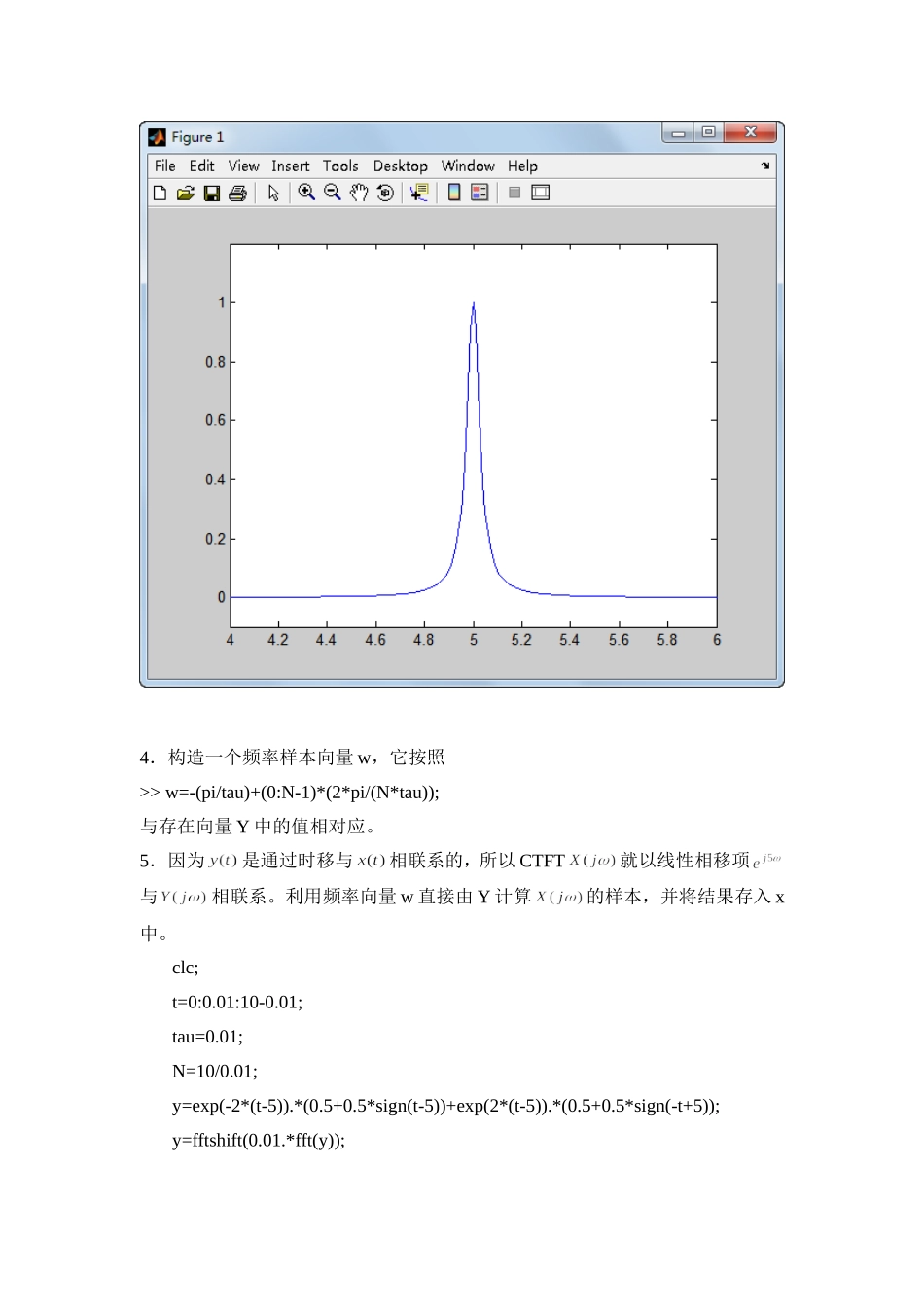
实验四连续时间傅立叶变换基本题1.求CTFT的解析表达式。可将看作,。g=sym('exp(-2*t)*Heaviside(t)');g2=subs(g,'-t','t');x=g+g2;fx=fourier(x);结果:fx=4/(4+w^2)2.创建一个向量,它包含了在区间t=[0:tau:T-tau]上(其中和),信号的样本。g=sym('exp(-2*t)*Heaviside(t)');g2=subs(g,'-t','t');x=g+g2;fx=fourier(x);clc;t=0:0.01:10-0.01;y=exp(-2*(t-5)).*(0.5+0.5*sign(t-5))+exp(2*(t-5)).*(0.5+0.5*sign(-t+5));plot(t,y);3.键入y=fftshift(tau*fft(y))计算样本。因为对于基本上为零,就能近似用个样本分析中计算出信号的CTFT。clc;t=0:0.01:10-0.01;y=exp(-2*(t-5)).*(0.5+0.5*sign(t-5))+exp(2*(t-5)).*(0.5+0.5*sign(-t+5));y=fftshift(0.01.*fft(y));y=abs(y);plot(t,y);axis([4,6,-0.1,1.2]);4.构造一个频率样本向量w,它按照>>w=-(pi/tau)+(0:N-1)*(2*pi/(N*tau));与存在向量Y中的值相对应。5.因为是通过时移与相联系的,所以CTFT就以线性相移项与相联系。利用频率向量w直接由Y计算的样本,并将结果存入x中。clc;t=0:0.01:10-0.01;tau=0.01;N=10/0.01;y=exp(-2*(t-5)).*(0.5+0.5*sign(t-5))+exp(2*(t-5)).*(0.5+0.5*sign(-t+5));y=fftshift(0.01.*fft(y));w=-(pi/tau)+(0:N-1)*(2*pi/(N*tau));x=exp(j*5*w).*y6.利用abs和angle画出在w标定的频率范围内X的幅值和相位。对于相同的值,也画出在1中所导出的解析式表达式的幅值和相位。CTFT的近似值与解析导得的相符吗?若想在一张对数坐标上画出幅值,可以用semilogy,这是会注意到,在较高的频率上近似不如在较低的频率上好。因为用了样本近似所以在时间段长度内,信号变化不大的那些信号的频率分量近似程度会更好一些。7.利用abs和angle画出Y的幅值和相位,它们与X的图比较后怎样?能估计到这一结果吗?§4.2连续时间傅立叶变换性质目的这个练习要借助于在频域和时域分析与操作声音信号来加深理解连续时间傅立叶变换CTFT。相关知识在MATLAB中声音信号是用含有连续时间声音信号样本的向量表示的,采样率定为8192Hz,也即声音信号是每隔采样一次。更仔细一些,对于一个声音信号,在区间上,以8192Hz采样,代表该声音信号的N个元素向量y由下式给出:然后,函数sound能用来在计算机的扬声器上放出该信号。虽然这是一个连续时间声音信号的采样表示,倘若在采样区间以外是零,而且采样率是足够快的,那么y就能认为是的一个准确表示在开始这个练习之前,必须首先装入一个采样的声音信号,这可键入>>loadsplat>>y=y(1:8192);为了确认已准确无误地装入了这个声音数据,并证实这个MATLAB向量y能正确地代表一个声音信号,可键入>>N=8192;>>fs=8192;>>sound(y,fs)函数fft取出该已采样的表示y,并在的样本点上计算近似的CTFT。若键入>>Y=fftshift(fft(y));那么向量Y就包含了区间上N个等分频率点处的近似值。事实上,Y包含的仅是的近似值,这里c是一个常数,但是不必担心这个近似,或这个加权系数,这仅是为本练习的需要而设定的。有关和Y之间关系的更为全面的讨论,请参考练习4.1。函数fftshift将fft的输出重新排序,以使得的样本在Y中的排序是从最负频率到最正的频率。现在,与CTFT有关的大多数性质都能在向量Y上得到证实。基本题1.键入Y=fftshift(fft(y)),计算向量Y的傅立叶变换。键入>>w=[-pi:2*pi/N:pi-pi/N]*fs;将对应的频率值存入向量w中。利用w和Y在区间内画出该连续时间傅立叶变换的幅值。函数ifft是fft的逆运算。对于偶数长度的向量,fftshift就是它本身的逆。对于向量Y,N=8192,这个逆傅立叶变换能用键入以下命令而求得>>y=ifft(fftshift(Y));>>y=real(y);由于原时域信号已知是实的,所以这里用了函数real。然而,在fft和ifft中的数值舍入误差都会在y中引入一个很小的非零虚部分量。一般说来,逆CTFT不必是一个实信号,而虚部可以包含有显著的能量。当已知所得信号一定是实信号时,并且已经证实所除掉的虚部分量是没有意义的,real函数才能用于ifft的输出上loadsplaty=y(1:8192);N=8192;fs=8192;Y=fftshift(fft(y));sound(y,fs);w=(-pi:2*pi/N:pi-pi/N)*fs;subplot(211)plot(w,Y);title('Y');y=ifft(fftshift(...