高中数学 142正弦函数、余弦函数的性质(1)课件 新人教A版必修4 课件VIP免费

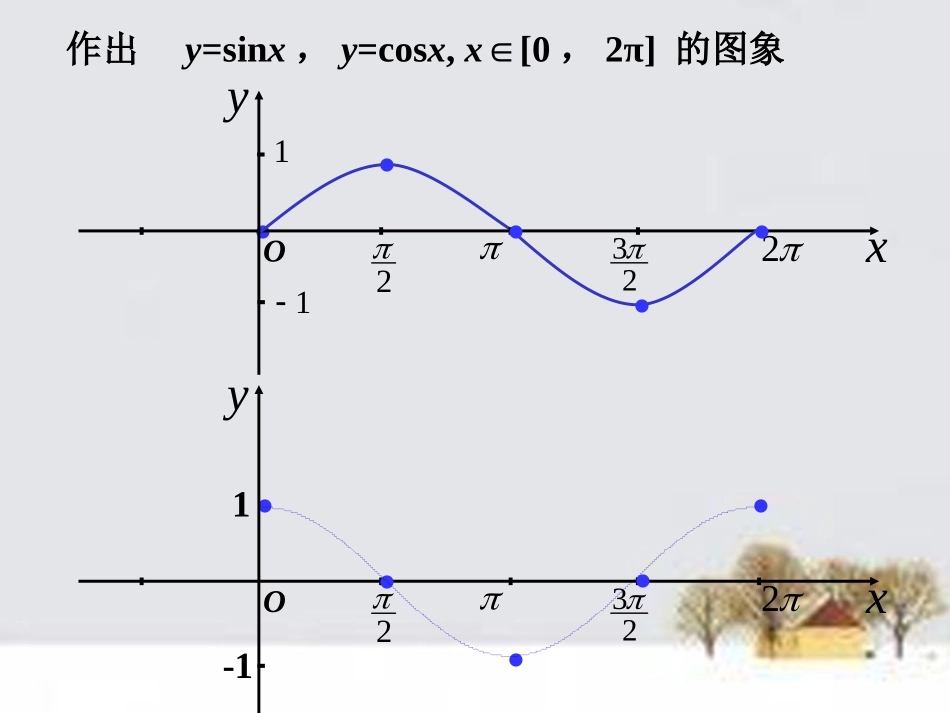
1.4.2正弦函数、余弦函数的性质（1）y=sinx、y=cosx的图象一、复习：22311.yxO2....作出y=sinx，y=cosx,x[0∈，2π]的图象223.yxO2....-11与x轴的交点(0,0)(,0)(2,0)图象的最高点2(,1)图象的最低点32(,1)与x轴的交点2(,0)32(,0)图象的最高点(0,1)(2,1)图象的最低点(,1)简图作法(五点作图法)(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)sin,[0,2]yxxcos,[0,2]yxxy=sinx、y=cosx的图象32532522322322-11yx0sin,yxxRcos,yxxR一、复习：余弦函数的图象正弦函数的图象y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同32532522322322-11yx032532522322322-11yx0sin,yxxRcos,yxxR下面我们研究正弦函数、余弦函数的主要性质．阅读教材第34页~37页（奇偶性之前）1.何为周期函数？2.如何求y=Asin(ωx+φ)和y=Acos(ωx+φ)的周期？回答问题：律：“周而复始”的变化规1.正弦函数和余弦函数的定义域、值域观察正弦曲线与余弦曲线，可以得出以下结论：y=sinx和y=cosx的定义域R32532522322322-11yx0sin,yxxR32532522322322-11yx0cos,yxxRy=sinx和y=cosx的值域[－1，1]都是__________.都是__________.2.正弦函数和余弦函数的周期性①从几何角度：观察正弦曲线，我们会发现，它在……[－4π,－2π)、[－2π,0)、[0,2π)、[2π,4π)……（这一特性从正弦线、余弦线的变化规律中也可以看出）22232232253253Rxxy，sin272744¦Èx0x1-122232232253253Rxxy，sin272744¦Èx0x1-1.cosRxxy，yy即x[2∈kπ,2(k+1)π)(k∈Z)上的图象是完全相同的.即自变量每相差2π，图象就“周而复始”重复出现.2.正弦函数和余弦函数的周期性32532522322322-11yx0sin,yxxRcos,yxxR②从代数式角度：sin(2kπ+x)=sinx(k∈Z)，cos(2kπ+x)=cosx(k∈Z).即对于函数y=sinx，y=cosx，自变量每增加（k>0）或减少(k<0)一个定值2kπ(k∈Z),函数值就重复出现.①从几何角度：观察正弦曲线，自变量每相差2π，图象就“周而复始”重复出现.（这一特性从正弦线、余弦线的变化规律中也可以看出）从这两个方面说明正弦函数和余弦函数具有周期性.周期函数的概念：对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.由定义有：正弦函数、余弦函数都是周期函数，对于一个周期函数f(x)，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.注意:1.T必须是非零常数；2.f(x+T)=f(x)必须对定义域内的每一个x值都成立.2kπ(k∈Z且k≠0)都是它们的周期.正弦函数、余弦函数最小正周期是2π.问：2sin()sin636等式是否成立？23能否说是正弦函数sinyxxR，的一个周期？答：2sin()635sin6sin()6sin62sin()sin636等式成立.2sin()sin3xx一个值都使等式成立2sin.3yx不是的周期R这个等式虽然成立，但不是对定义域内的每正弦函数、余弦函数的性质：函数y＝sinxy＝cosx图象定义域值域__________________奇偶性_________________周期性最小正周期：___最小正周期：____[－1,1][－1,1]奇函数偶函数2π2πRR.1例求下列函数的周期：(1)3cosyxxR，；(2)sin2yxxR，；解：3cos2yx的周期是；(2)sin(22)sin2,()xxxRsin2()sin2xxxR即，sin2yx的周期是；1(3)2sin().26yxxR，(1)3cos(2)3cos,()xxxR11(3)2sin(2)2sin(),()2626xxxR112sin[(4)]2sin(),()2626xxxR即12...