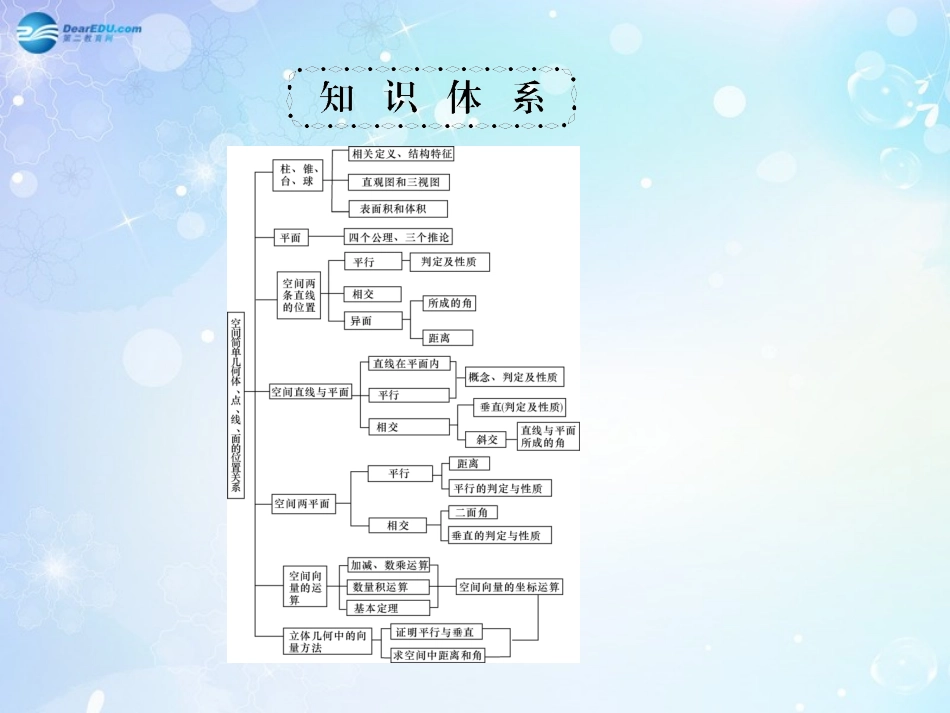
第八章直线、平面、简单几何体和空间向量理解以下判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.理解以下性质定理,并能够证明之:如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.如果两个平行平面同时和第三个平面相交,那么它们的交线互相平行.垂直于同一个平面的两条直线平行.如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.第54讲空间几何体的结构特征和其三视图与直观图【学习目标】1.认识柱、锥、台、球及其简单组合体的结构特征,掌握柱、锥的简单几何体性质.2.了解空间图形的两种不同表示形式(三视图和直观图),了解三视图、直观图与它们所表示的立体模型之间的内在联系.3.能画出简单空间图形及实物的三视图与直观图,能识别三视图所表示的立体模型,会用斜二测画法画出它们的直观图.4.会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图.【基础检测】1.下列命题正确的是()A.直平行六面体是长方体B.对角面是全等的平行四边形的四棱柱是长方体C.侧面为矩形的直四棱柱是长方体D.底面是矩形的直四棱柱是长方体【解析】直平行六面体的底面不一定是矩形;对角面是全等的平行四边形的四棱柱,底面可以是等腰梯形,不是长方体;侧面为矩形的直四棱柱底面不一定是矩形,故选D.D2.以下命题①用一个平面去截棱锥,底面和截面之间的部分叫棱台;②将一个直角三角形绕其一条直角边旋转一周,所得圆锥的母线长等于斜边长;③棱台的相对侧棱延长后必交于一点;④用一平面去截球,所得截面圆圆心和球心的连线一定与截面垂直.其中正确命题的个数为()A.1B.2C.3D.4【解析】②③④正确,①错误,故选C.C3.给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台的上、下底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是相互平行的.其中正确的是()A.①②B.②③C.①③D.②④D4.若某几何体的三视图如图所示,则这个几何体的直观图可以是()【解析】从俯视图看,B和D符合,从正视图看D符合,而从侧视图看D也是符合的.D【解析】由直观图与原图形中边OB长度不变,由S原图形=22S直观图,有12·OB·h=22×12×2·O′B′,∴h=42.5.如图所示,△A′O′B′表示水平放置的△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=2,则△AOB的边OB上的高为_______.42【知识要点】1.空间几何体的结构特征多面体棱柱棱柱的侧棱都相互____且____,上下底面是_______且________的多边形.棱锥棱锥的底面是任意多边形,侧面是有一个________的三角形.棱台棱台可由一个_____________________得到,其上下底面是________且相似的多边形.平行相等全等的相互平行公共顶点平行于棱锥底面的平面去截棱锥相互平行旋转体圆柱圆柱可由_______绕其任意一边旋转得到.圆锥圆锥可以由___________绕其一条直角边旋转得到.圆台圆台可以由直角梯形绕直角腰或等腰梯形绕上下边的中点连线旋转得到,也可由_________圆锥底面的平面截圆锥得到.球球可以由半圆或圆绕其_______旋转得到.矩形直角三角形平行于直径2.三视图空间几何体的三视图由平行投影得到,这种投影下,与投影面平行的平面图形留下的影子,与平面图形的形状和大小是全等和相等的,三视图包括_____________、_________、_________.3.空间几何体的直观图空间几何体的直观图常用斜二测画法来画,基本步骤是:(1)画几何体的底面在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′=45°,已知图形中平行于x轴、y轴的线段在直观图中平行于x′轴、y′轴;已知图形中平行于x...