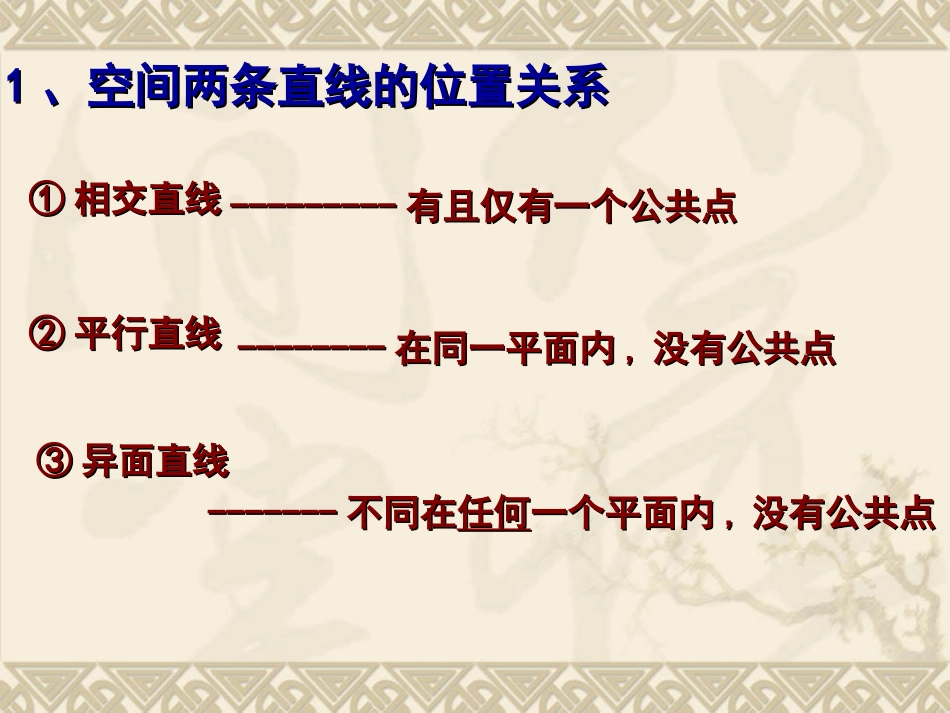
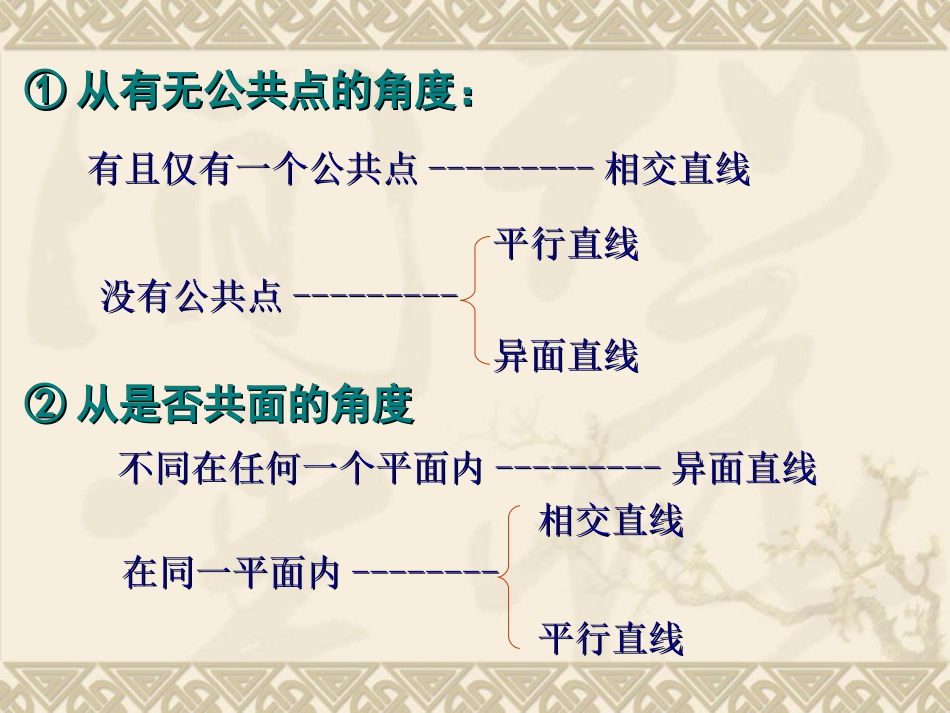
§2.1.2§2.1.2空间中直线与直线空间中直线与直线之间的位置关系之间的位置关系(1)(1)11、空间两条直线的位置关系、空间两条直线的位置关系①①相交直线相交直线②②平行直线平行直线③③异面直线异面直线------------------有且仅有一个公共点有且仅有一个公共点----------------在同一平面内在同一平面内,,没有公共点没有公共点--------------不同在不同在任何任何一个平面内一个平面内,,没有公共点没有公共点①①从有无公共点的角度:从有无公共点的角度:有且仅有一个公共点有且仅有一个公共点------------------相交直线相交直线在同一平面内在同一平面内----------------相交直线相交直线②②从是否共面的角度从是否共面的角度没有公共点没有公共点------------------平行直线平行直线异面直线异面直线不同在任何一个平面内不同在任何一个平面内------------------异面直线异面直线平行直线平行直线异面直线的画法异面直线的画法αab图1αβba图2αab图3这样表示这样表示aa、、bb异面正确吗?异面正确吗?αβbaA1B1C1D1ABCD如图:AA1与CC1在同一平面吗?直观上理论上在图中找出另外的一些异面直线BB1∥AA1,DD1∥AA1,BB1与DD1平行吗?2、平行直线公理4平行同一条直线的两条直线互相平行.设设aa,,bb,,cc为直线为直线a∥bc∥ba∥caabbccaa,,bb,,cc三条直线两两平行,可以记为a∥b∥c符号语言(空间平行线的传递性)AcBDEFGH例1、已知四边形ABCD是空间四边形,E、H分别是边AB、AD的中点,F、G分别是边CB、CD上的中点,求证:四边形EFGH是平行四边形.AcBDEFGH例2、已知四边形ABCD是空间四边形,E、H分别是边AB、AD的中点,F、G分别是边CB、CD上的点,且==。求证:四边形EFGH有一组对边平行但不相等CFCBCGCD23ABCDEPMN例3、如图,P是△ABC所在平面外一点,D、E分别是△PAB和△PBC的重心。求证:DE∥AC,DE=AC131、一条直线与两条异面直线中的一条相交,那么它与另一条之间的位置关系是()A、平行B、相交C、异面D、可能平行、可能相交、可能异面2、两条异面直线指的是()A、没有公共点的两条直线B、分别位于两个不同平面的两条直线C、某一平面内的一条直线和这个平面外的一条直线D、不同在任何一个平面内的两条直线练习:3、两条直线不相交是这两条直线异面的条件_______.4、两条直线不平行是这两条直线异面的条件5、下列命题中,其中正确的是(1)若两条直线没有公共点,则这两条直线互相平行(2)若两条直线都和第三条直线相交,那么这两条直线互相平行(3)若两条直线都和第三条直线平行,那么这两条直线互相平行(4)若两条直线都和第三条直线异面,那么这两条直线互相平行6、三个平面两两相交,所得的三条交线()A、交于一点B、互相平行C、有两条平行D、或交于一点或互相平行小结①①从有无公共点的角度:从有无公共点的角度:有且仅有一个公共点有且仅有一个公共点------------------相交直线相交直线在同一平面内在同一平面内----------------相交直线相交直线②②从是否共面的角度从是否共面的角度没有公共点没有公共点------------------平行直线平行直线异面直线异面直线不同在任何一个平面内不同在任何一个平面内------------------异面直线异面直线平行直线平行直线空间直线空间直线公理4平行同一条直线的两条直线互相平行