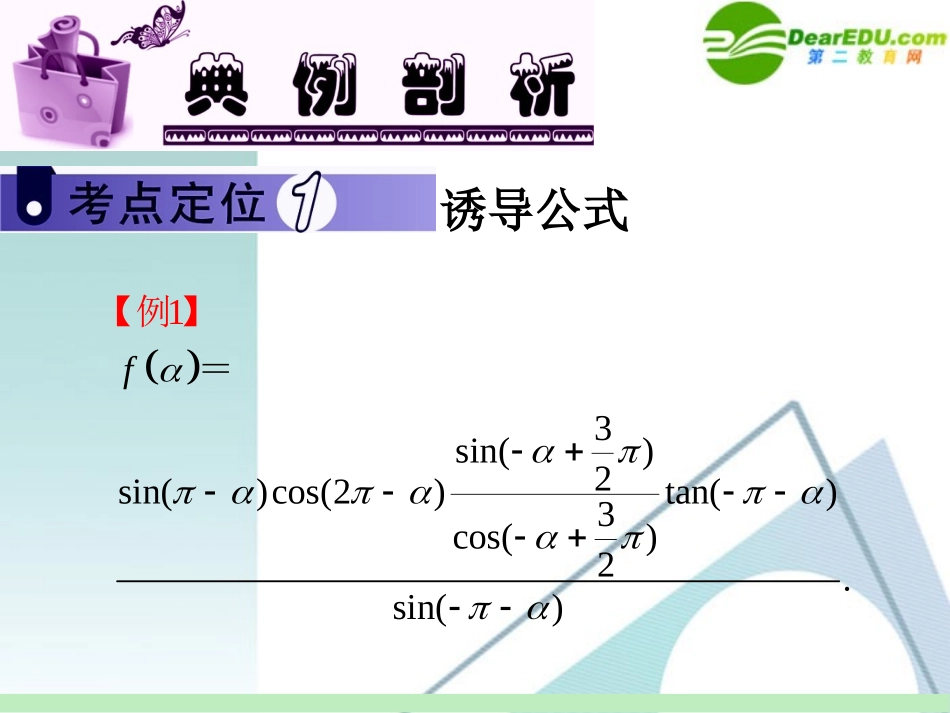
诱导公式3sin()2sin()cos(2)tan()3cos()2.sin1()f例=【】1312cos()2531860fff化简;若是第三象限角,且-=,求的值;若=-,求的值.sinsin()cos()(tan)cossin()cos.311cos()sin.25526cos.526.5(1860)cos(1860)c12os18601cos(536060)cos60.32fff==-由-=,得=-又是第三象限角,所以=-所以=-=--=-=-+=-【=-解析】本题主要考查诱导公式.应用诱导公式,重点是“函数名称”与“正负号”的正确判断.求任意角的三角函数值的问题,都可以通过诱导公式化为锐角三角函数的求值问题.具体步骤为“负角化正角→正角化锐角→求值”.8tan()(1)71513sin()3cos()77_________2022sin()cos()717mm【变式练习】设+=,则=8tan()tan().771513sin()3cos()772022sin()cos()77sin()3cos()77sin()cos()77337117mmtanmmtan【解析+=,+=故原式====】同角三角函数之间的基本关系式2tan31sinsin2cos25cos3sin33cos3sinc2os1.已知=,求下列各式的值.;;-例+【】22sin3tan3cossincos1310sin.10310sin;10310sin11.0由=,得,解得=当在第一象限时,=当在第三象限时,=-【解析】222222222sin2costan2321.5cos3sin53tan533143cos3sincos14cos3sincossin4cos3sincossinsincos43tantan42.tan211305===-+=-+====本题利用同角三角函数之间的基本关系,由一个角的某个三角函数值求该角的另外的三角函数值.注意角的范围,同时对于(2)(3)注意弦化切的思想.2211cos1tan3tan2已知=,求【变式练习+】+的值.2221cos38sintan8311731tan18.tan88【解由=,得=,=,所以++=++=析】化简、求值、证明2210sincos.251sincos3sin2sincoscos22222tancot3xxxxxxxxxxx已知-,+=求:-的值;【例】的值.2221sincos51(sincos)()5242sincos.2549(sincos)12sincos,250sin0cos027sinc1os.5xxxxxxxxxxxxxxx由+=,得+=,所以=-因为-=-=又-,所【以,,所以-=-解析】2223sin2sincoscos2222tancot2sinsin12sincoscossinsincos(2cossin)121108(2).2551225xxxxxxxxxxxxxxxx==--=--=-在三角函数变换与求值中,已知sinα+cosα,sinαcosα,sinα-cosα中的一个可利用方程的思想求出另外两个的值.解题时,要特别注意开方后正负号的取舍,这要依据已知条件确定sinα与cosα的大小关系:当α的终边落在直线y=x上时,sinα=cosα;当α的终边落在直线y=x的上半平面区域内时,sinα>cosα;当α的终边落在直线y=x的下半平面区域内时,sinα