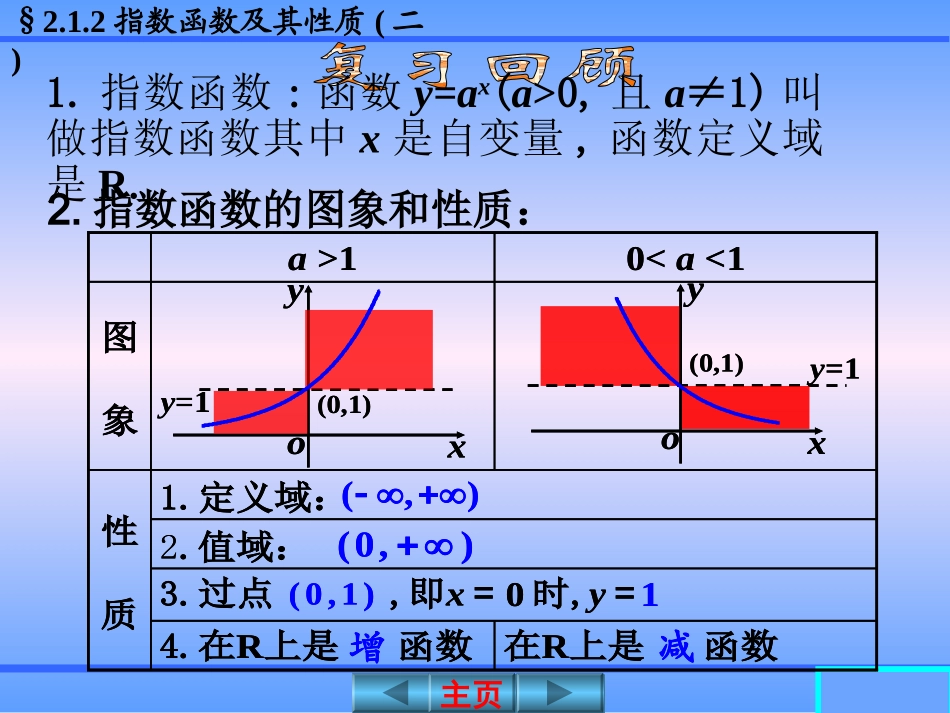
§2.1.2指数函数及其性质(二)主页主页1.指数函数:函数y=ax(a>0,且a≠1)叫做指数函数其中x是自变量,函数定义域是R.2.指数函数的图象和性质:在R上是函数4.在R上是函数3.过点,即x=时,y=2.值域:1.定义域:性质图象0
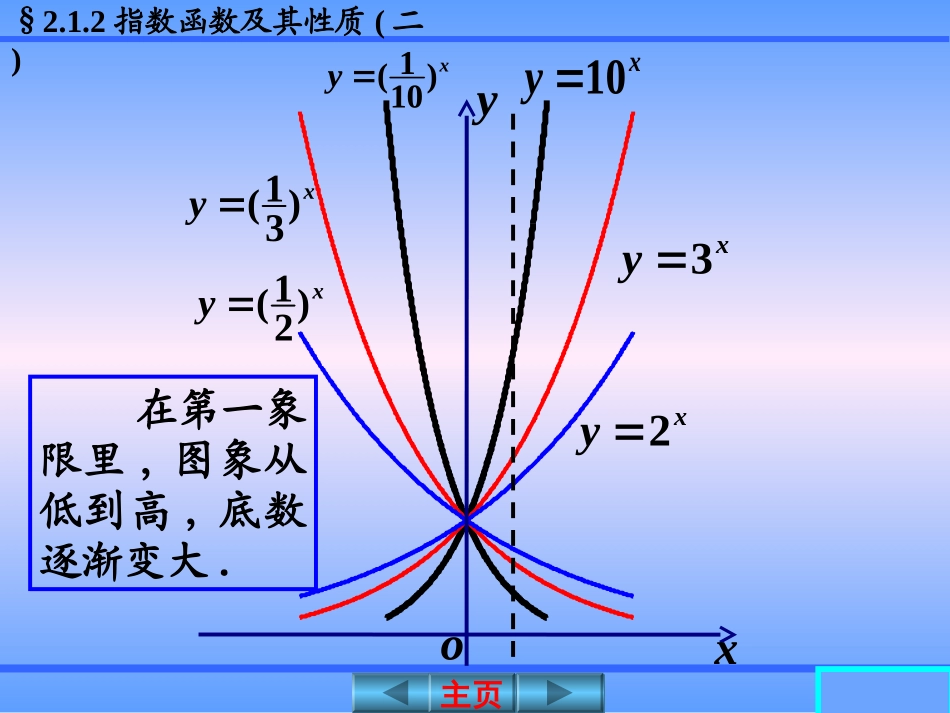
1(,)(0,)(0,1)yxoy=1(0,1)yx(0,1)y=1o01增减在R上是函数4.在R上是函数3.过点,即x=时,y=2.值域:1.定义域:性质图象01(,)(0,)(0,1)yxoy=1(0,1)yx(0,1)y=1o01增减§2.1.2指数函数及其性质(二)主页主页xoy2xy1()10xy3xy10xy1()3xy1()2xy在第一象限里,图象从低到高,底数逐渐变大.§2.1.2指数函数及其性质(二)主页主页【3】在同一坐标系下,函数y=ax,y=bx,y=cx,y=dx的图象如下图,则a,b,c,d,1之间从小到大的顺序是__________________.xoyxyaxybxycxydxoyxyaxybxycxyd1badc§2.1.2指数函数及其性质(二)主页主页【4】指数函数满足不等式,则它们的图象是().(),(),xxfxmgxn①②C.A.B.D.xoy①②xoy①②xoy②①xoy②①xoy①②xoy①②xoy②①xoy②①01nmD§2.1.2指数函数及其性质(二)主页主页【3】已知函数f(x)是奇函数,且当x>0时,f(x)=2x+1,求当x<0时,f(x)的解析式.又因为f(x)是奇函数,∴f(-x)=-f(x).解:因为当x>0时,∴当x<0时,-x>0,即1,()2xfx1.()2xxf1,()2xxf1.()2xxf所以当x<0时,-1.()2xfxxoy-22xoy-22§2.1.2指数函数及其性质(二)主页主页图像过定点问题例2.函数y=ax-3+2(a>0,且a≠1)必经过哪个定点?点评:函数y=ax-3+2的图象恒过定点(3,3),实际上就是将定点(0,1)向右平移3个单位,向上平移2个单位得到.由于函数y=ax(a>0,且a≠1)恒经过定点(0,1),因此指数函数与其它函数复合会产生一些丰富多彩的定点问题(3,3)§2.1.2指数函数及其性质(二)主页主页【1】函数y=ax+5-1(a>0,且a≠1)必经过哪个定点?2.图像过定点问题【2】函数恒过定点(1,3)则b=____.2xbya(5,0)1§2.1.2指数函数及其性质(二)主页主页例4.设a是实数,(1)试证明对于任意a,f(x)为增函数;2().21xfxa证明:任取x1,x2,且f(x1)-f(x2)=21222121xx12212222(21)(21)xxxx12212(22).(21)(21)xxxx y=2x在R上是增函数,且x1<x2,1222,xx12210,210,xx又12220.xx即∴f(x1)-f(x2)<0,即f(x1)<f(x2).故对于a取任意实数,f(x)为增函数.4.单调性与奇偶性问题12.xx§2.1.2指数函数及其性质(二)主页主页解:若f(x)为奇函数,则f(-x)=-f(x),22(),2121xxaa即22221221xxxa22212xx.2利用f(0)=0例4.设a是实数,(2)试确定a的值,使f(x)为奇函数.2().21xfxa∴a=1.§2.1.2指数函数及其性质(二)主页主页【1】已知定义域为R的函数为奇函数,则a=__,b=_____.1-2()2xxbfxa21【2】设a>0,在R上为偶函数,(1)求a,(2)证明函数f(x)在(0,+∞)上为增函数.e()exxafxa(0)01;fb(1)(1)2.ffa1212121()-()(e-e)(-1)exxxxfxfx1211212-1-ee(e-1)exxxxxxx§2.1.2指数函数及其性质(二)主页主页例1.讨论函数的单调性,并求其值域.221()(),15xxfxx≤解:任取x1,x2∈(-∞,1],且x10,f(x2)>0,2222112221()1()()5xxxxfxfx指数形式的复合函数的单调性(奇偶性)则2121()(2)1().5xxxx§2.1.2指数函数及其性质(二)主页主页 x10,x1+x2-2<0.2121()(2)011()()55xxxx§2.1.2指数函数及其性质(二)主页主页例2.求证函数是奇函数,并求其值域.1.指数形式的复合函数的单调性(奇偶性)101()101xxfx证明:函数的定义域为R,所以f(x)在R上是奇函数.101()101xxfx10(101)10(101)xxxx110110xx().fx§2.1.2指数函数及其性质(二)主页主页例2.求...