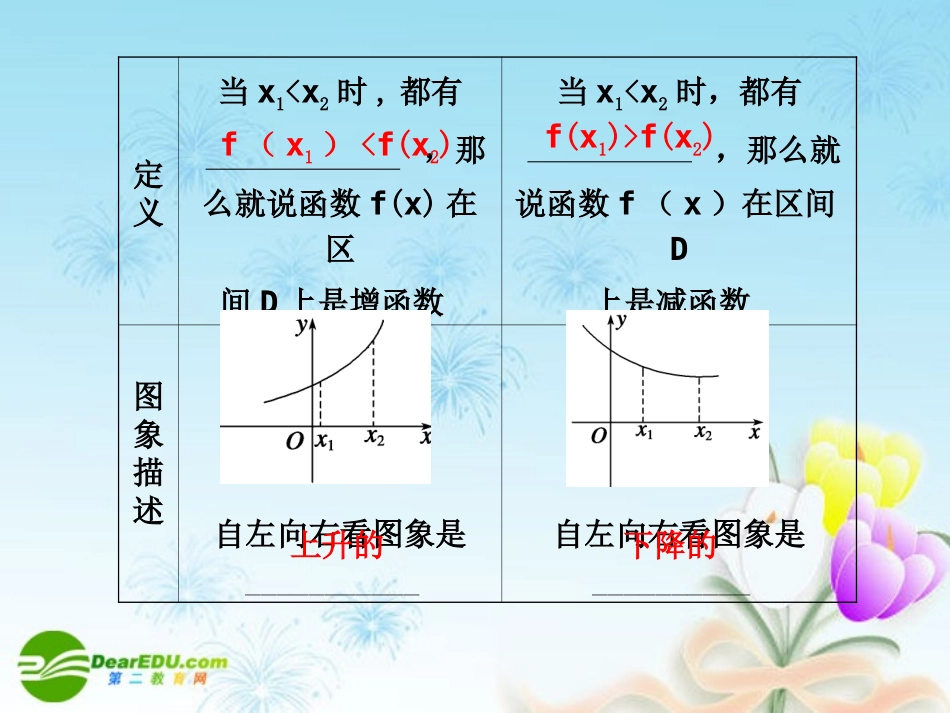
§2.3函数的单调性基础知识自主学习要点梳理1.函数的单调性(1)单调函数的定义增函数减函数定义一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量x1,x2定义当x1f(x2)上升的下降的(2)单调区间的定义若函数f(x)在区间D上是________或________,则称函数f(x)在这一区间上具有(严格的)单调性,________叫做f(x)的单调区间.增函数减函数区间D2.函数的最值前提设函数y=f(x)的定义域为I,如果存在实数M满足条件①对于任意x∈I,都有___________;②存在x0∈I,使得_____________.①对于任意x∈I,都有____________;②存在x0∈I,使得_______________.结论M为最大值M为最小值f(x)≤Mf(x0)=Mf(x)≥Mf(x0)=M基础自测1.下列函数中,在区间(0,2)上为增函数的是()A.y=-x+1B.y=C.y=x2-4x+5D.解析 y=-x+1,y=x2-4x+5,分别为一次函数、二次函数、反比例函数,从它们的图象上可以看出在(0,2)上都是减函数.xy2Bxy2x2.已知函数y=f(x)是定义在R上的增函数,则f(x)=0的根()A.有且只有一个B.有2个C.至多有一个D.以上均不对解析 f(x)在R上是增函数,∴对任意x1,x2∈R,若x10;②(x1-x2)[f(x1)-f(x2)]<0;③④其中能推出函数y=f(x)为增函数的命题为______.解析依据增函数的定义可知,对于①③,当自变量增大时,相对应的函数值也增大,所以①③可推出函数y=f(x)为增函数.;0)()(2121xxxfxf.0)()(2121xxxfxf①③题型分类深度剖析题型一函数单调性的判断判断下列函数的单调性,并证明.先判断单调性,再用单调性的定义证明.(1)采用通分进行变形,(2)采用因式分解进行变形,(3)采用分子有理化的方式进行变形.【例1】).,1[,1)()3();,1[,12)()2();,1(,12)()1(2xxxfxxxxfxxxf思维启迪解(1)函数下面采用定义证明:任取x1、x2∈(-1,+∞),且-10,x2+1>0,x2-x1>0.即f(x1)-f(x2)>0,所以f(x1)>f(x2)..),1(12)(上为减函数在xxf,)1)(1()(21212)()(21122121xxxxxxxfxf,0)1)(1()(22112xxxx故在(-1,+∞)上为减函数.(2)函数f(x)=-x2+2x+1在[1,+∞)上为减函数,证明如下:任取x1、x2∈R,且x2>x1≥1,则f(x1)-f(x2)==(x2+x1)(x2-x1)+2(x1-x2)=(x2-x1)(x2+x1-2). x2>x1≥1,∴x2-x1>0,x2+x1>2,x2+x1-2>0,∴f(x1)-f(x2)=(x2-x1)(x2+x1-2)>0,即有f(x1)>f(x2).12)(xxf)12()12(222121xxxx)(2)(212122xxxx故函数f(x)=-x2+2x+1在[1,+∞)上是减函数.(3)函数f(x)=在[-1,+∞)上为增函数,证明如下:任取x1、x2∈[-1,+∞)且-1≤x1