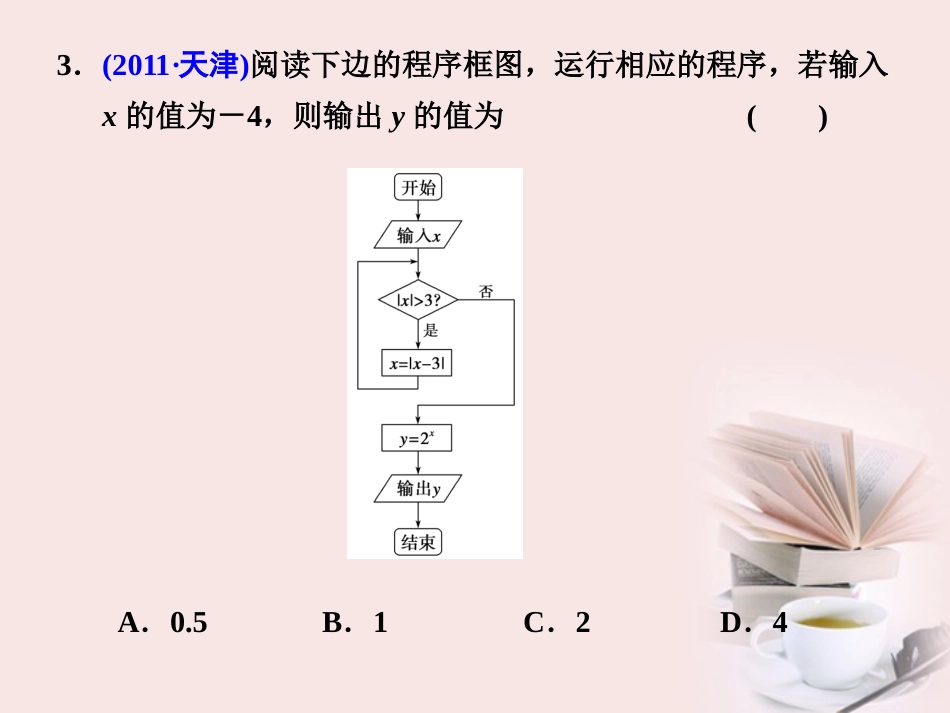
§4算法初步、复数真题热身1.(2011·课标全国)复数2+i1-2i的共轭复数是()A.-35iB.35iC.-iD.i解析方法一 2+i1-2i=(2+i)(1+2i)(1-2i)(1+2i)=2+i+4i-25=i,∴2+i1-2i的共轭复数为-i.方法二 2+i1-2i=-2i2+i1-2i=i(1-2i)1-2i=i.∴2+i1-2i的共轭复数为-i.C2.(2011·湖北)i为虚数单位,则1+i1-i2011等于()A.-iB.-1C.iD.1解析 1+i1-i=(1+i)2(1-i)(1+i)=i,∴1+i1-i2011=i2011=i4×502+3=i3=-i.A3.(2011·天津)阅读下边的程序框图,运行相应的程序,若输入x的值为-4,则输出y的值为()A.0.5B.1C.2D.4解析当x=-4时,|x|=4>3,x赋值为x=|-4-3|=7>3,∴x赋值为x=|7-3|=4>3,x再赋值为x=|4-3|=1<3,则y=21=2,输出2.答案C4.(2011·山东)执行如图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是________.解析当输入l=2,m=3,n=5时,不满足l2+m2+n2=0,因此执行:y=70l+21m+15n=70×2+21×3+15×5=278.由于278>105,故执行y=y-105,执行后y=278-105=173,再执行一次y=y-105后y的值为173-105=68,此时68>105不成立,故输出68.答案68考点整合1.算法初步(1)程序框图的三种逻辑结构顺序结构、条件结构、循环结构.(2)程序设计语言的基本算法语句任何一种程序设计语言都包含五种基本的算法语句,分别是输入语句、输出语句、赋值语句、条件语句、循环语句.(3)循环结构分为当型循环结构和直到型循环结构:①当型循环结构:先判断给定的条件p是否成立,若成立,则执行操作A,再判断给定的条件p是否成立,若成立,再执行操作A,如此反复,直到条件p不成立,退出循环.②直到型循环结构:先执行操作A,再判断给定的条件p是否成立,若不成立,则执行操作A,如此反复,直到条件p成立,退出循环.2.复数(1)形如a+bi(a、b∈R)的数叫复数.①复数是实数的条件:a.z=a+bi(a,b∈R)∈R⇔b=0;b.z∈R⇔z=z;c.z∈R⇔z2≥0.②复数是纯虚数的条件:a.z=a+bi(a,b∈R)是纯虚数⇔a=0且b≠0;b.z是纯虚数⇔z+z=0(z≠0);c.z是纯虚数⇔z2<0.(2)复数相等是沟通复数与实数的桥梁,通过它把复数问题实数化:若a+bi=c+di(a、b、c、d∈R)⇔a=c,b=d.(3)复数的加、减、乘法类似于实数运算,除法分母实数化,最终结果化为a+bi(a、b∈R)的形式.复数的运算常用的结论:i2=-1,i4n+1=i,i4n+2=-1,i4n+3=-i,i4n=1(n∈Z);in+in+1+in+2+in+3=0(n∈Z);(1±i)2=±2i,1+i1-i=i,1-i1+i=-i.分类突破一、复数的概念例1(1)设z2=z1-iz1(其中z1表示z1的共轭复数),已知z2的实部是-1,则z2的虚部为________.解析设z1=x+yi,z2=-1+bi,则-1+bi=x+yi-i(x-yi)=(x-y)+(y-x)i,由复数相等得-1=x-y,b=y-x,∴b=1.1(2)在复平面内,复数z=sin2+icos2对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限解析因为sin2>0,cos2<0,所以z=sin2+icos2对应的点在第四象限.D归纳拓展(1)解决复数问题的指导思想是化归思想,就是把复数问题转化成实数来解决,可设复数z=a+bi(a,b∈R),通过研究实数a,b来体现复数z的特点.(2)因为复数由它的实部与虚部唯一确定,所以可将复数与复平面的点联系起来,这就是复数的几何意义.此外,复数还可与向量、三角函数等知识联系.变式训练1(1)下面四个命题:①0比-i大;②两个复数互为共轭复数,当且仅当其和为实数;③x+yi=1+i的充要条件为x=y=1;④如果让实数a与ai对应,那么实数集与纯虚数集一一对应.其中正确命题的个数是()A.0B.1C.2D.3解析①中实数与虚数不能比较大小;②两个复数互为共轭复数时其和为实数,但两个复数的和为实数时这两个复数不一定是共轭复数;③x+yi=1+i的充要条件为x=y=1是错误的,因为没有标明x,y是否是实数;④当a=0时,没有纯虚数和它对应.A(2)若θ∈34π,54π,则复数(cosθ+sinθ)+(sinθ-cosθ)i在复平面内所对应的点在第________象限.解析 cosθ+sinθ=2sin...