高中数学 234平面与平面垂直的性质课件 新人教A版必修2 课件VIP免费

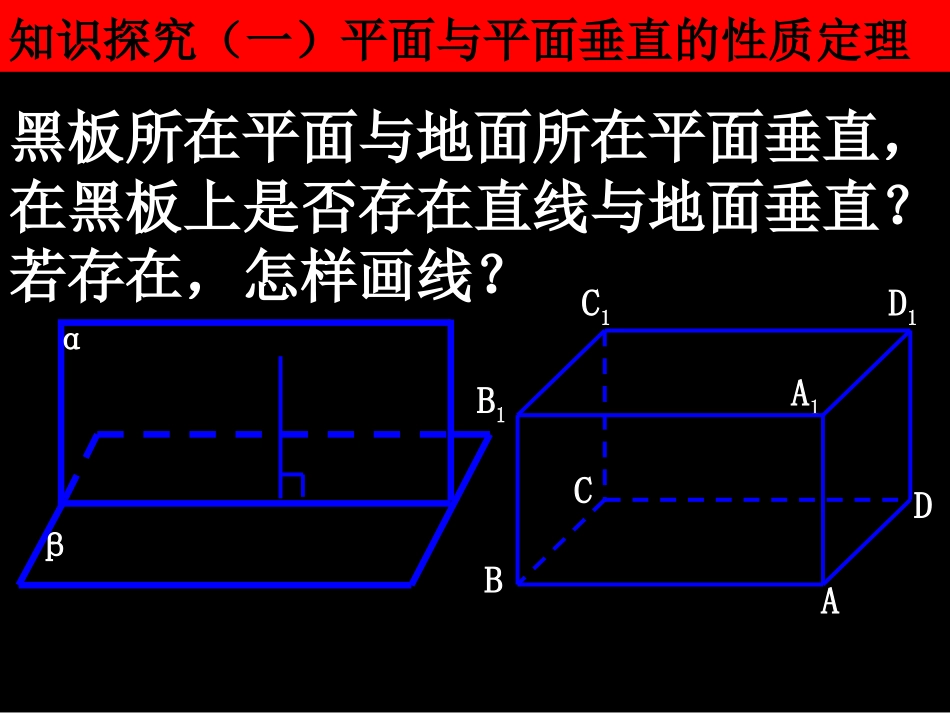
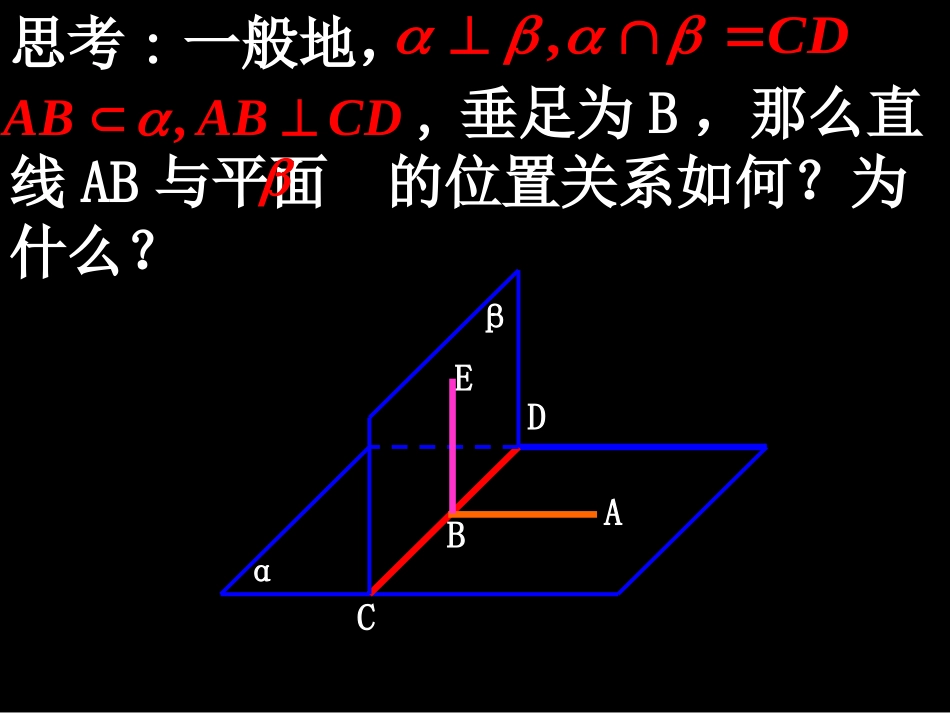
知识探究（一）平面与平面垂直的性质定理黑板所在平面与地面所在平面垂直，在黑板上是否存在直线与地面垂直？若存在，怎样画线？αβAA1BCDB1C1D1思考:一般地，,垂足为B，那么直线AB与平面的位置关系如何？为什么？,CD,ABABCDαβABDCE据上分析可得什么定理？试用文字语言表述之.定理两个平面互相垂直，则在一个平面内垂直交线的直线与另一个平面垂直.αβABDCαβlm,,,.lmlml知识探究（二）平面与平面垂直的性质探究思考1:若α⊥β，过平面α内一点A作平面β的垂线，垂足为B，那么点B在什么位置？说明你的理由.BαβA上述分析表明：如果两个平面互相垂直，那么经过一个平面内一点且垂直于另一个平面的直线，必在这个平面内BαβA理论迁移例1如图，已知α⊥β，l⊥β，，试判断直线l与平面α的位置关系，并说明理由.lαβlma思考3:对于三个平面α、β、γ，如果α⊥γ，β⊥γ，，那么直线l与平面γ的位置关系如何？为什么？lαβγlab思考4:上述结论如何用文字语言表述？该性质在实际应用中有何理论作用？如果两个相交平面都垂直于另一个平面，那么这两个平面的交线垂直于这个平面.αβγl例2如图，四棱锥P-ABCD的底面是矩形，AB=2，，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD.（1）证明：侧面PAB⊥侧面PBC；2BC（2）求侧棱PC与底面ABCD所成的角.PABCDE例2如图，四棱锥P-ABCD的底面为矩形，PA⊥底面ABCD，PA=AD，M为AB的中点，求证：平面PMC⊥平面PCD.PABCDMEF