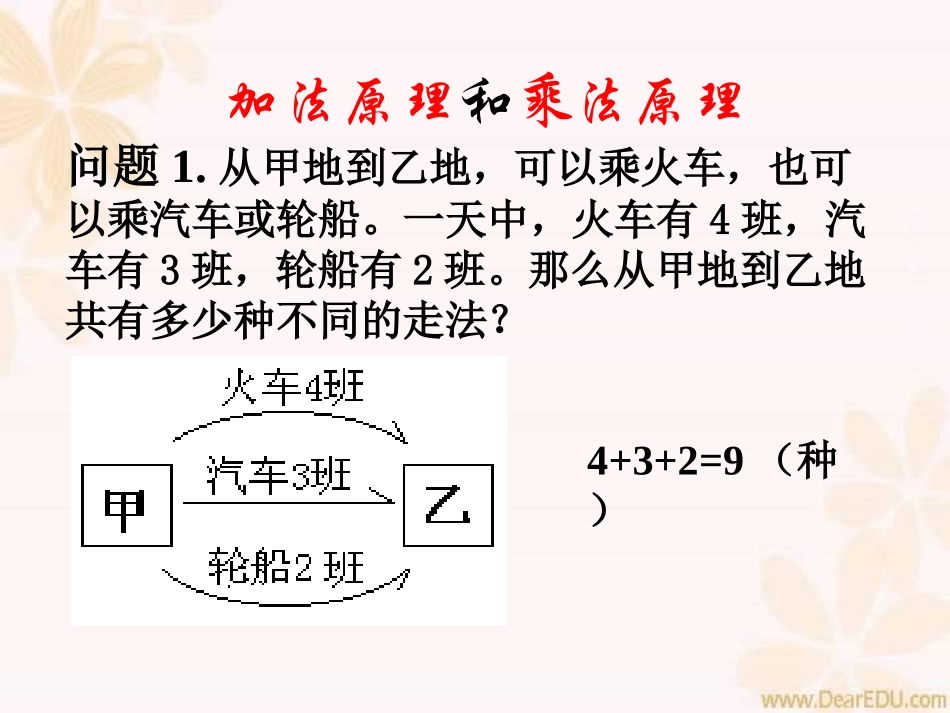
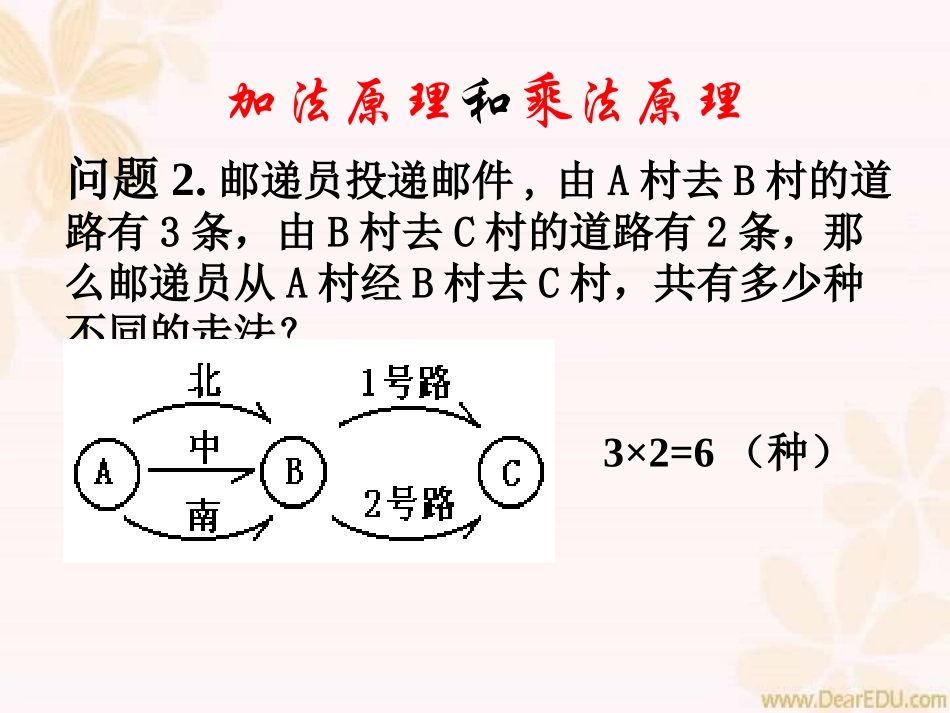
问题1.从甲地到乙地,可以乘火车,也可以乘汽车或轮船。一天中,火车有4班,汽车有3班,轮船有2班。那么从甲地到乙地共有多少种不同的走法?加法原理和乘法原理4+3+2=9(种)如果完成一件工作,有几类方法,那么完成这件工作的方法的总和等于各类中完成这件工作的方法种数的和。加法原理请你用加法原理说明(1)图书室有150本不同的科技书,200本不同的童话书,100本不同的漫画,你想借一本共有多少种不同的选法?(2)老师要从4个男生,5个女生中任选一人担任组长,共有多少种不同的选取法?问题2.邮递员投递邮件,由A村去B村的道路有3条,由B村去C村的道路有2条,那么邮递员从A村经B村去C村,共有多少种不同的走法?加法原理和乘法原理3×2=6(种)如果要完成一件工作,要分几步完成,那么完成这件工作的方法总数等于完成各步的方法种数的积。乘法原理请用乘法原理说明(1)某人到食堂买饭,主食有3种,副食有5种,他主食和副食各买一种,共有多少种不同的买法?(2)在自然数中,用两位数做被减数,用一位数做减数,共可以组成多少个不同的减法算式?不同点:(加法原理)一步完成,分几类去思考;(乘法原理)分几步完成,分步去思考。加法原理和乘法原理想一想:在解决下列问题时,用的是什么原理?为什么?(1)有5个不同的文具盒,4支不同的铅笔,3块不同的橡皮,2把不同的尺子,若从中各取一个,配成一套学习用具,最多有多少套不同的学习用具?(2)有不同的语文书5本,数学书6本,英语书3本,自然书2本。从中任取一本,共有多少种不同的取法?想一想:在解决下列问题时,用的是什么原理?为什么?(3)一个口袋内装有3个不同的小球,另一个口袋内有8个不同的小球,从两个口袋内任取一个小球,有多少种不同的取法?(4)一个口袋内装有3个不同的小球,另一个口袋内有8个不同的小球,从两个口袋内各取一个小球,有多少种不同的取法?想一想:在解决下列问题时,用的是什么原理?为什么?(5)如图,从甲地到丙地共有多少种不同的走法?(6)某铁路局从A站到B站共有5个火车站(包括A和B),铁路局要为这条铁路线准备几种不同的车票?甲甲乙丙综合应用:1、由1、2、3、4这4个数字组成的不含重复数字的三位数有多少个?2、如图:一只小甲虫要从A点出发沿着线段爬到B点,要求任何点和线段不可重复经过。问:这只甲虫有多少种不同的走法?ADCB3、从1—9这九个数字中,每次取两个数字,这两个数字的和必须大于10,那么共有几种取法?4、直线上有100个点,以每两点为端点的线段有多少条?请用已学知识具体说明为什么某些城市的电话号码要从七位变成八位?