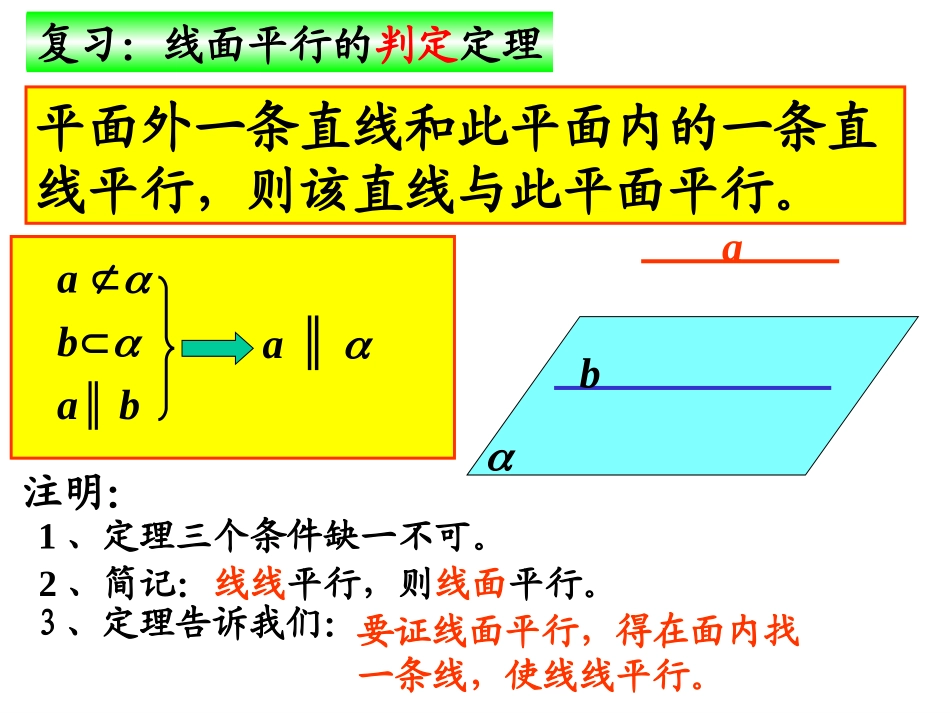
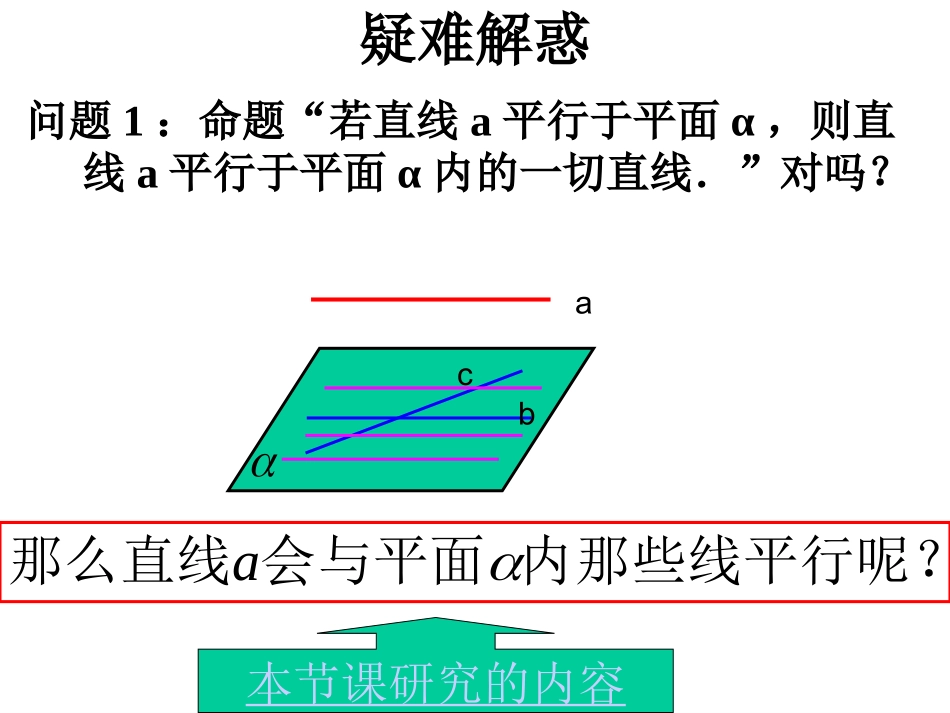
复习:线面平行的判定定理平面外一条直线和此平面内的一条直线平行,则该直线与此平面平行。baba∥baa∥注明:1、定理三个条件缺一不可。2、简记:线线平行,则线面平行。3、定理告诉我们:要证线面平行,得在面内找一条线,使线线平行。疑难解惑问题1:命题“若直线a平行于平面α,则直线a平行于平面α内的一切直线.”对吗?abca那么直线会与平面内那些线平行呢?本节课研究的内容2ba问题:在上面的论述中平面的直线满足什么条件时可以与直线平行?aaa与平面的任何直线都没有公共点,过直线的某一个平面,若与平面相交,则直线就平行于这一条交线。ba,,//aabab已知:直线求证:证明://aa与没有公共点b又因为在内ab与没有公共点ab又与都在平面内且没有公共点//ab新课:直线和平面平行的性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。ba//ba注意:1、定理三个条件缺一不可。2、简记:线面平行,则线线平行。,,aab例2:有一块木料如图,已知棱BC平行于面A′C′.(1)要经过木料表面A′B′C′D′内的一点P和棱BC将木料锯开,应怎样画线?(2)所画的线和面AC有什么关系?演示课件演示课件例题:已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面aba//ba//abb如图:已知直线,,平面,且,,,都在平面外。求证://ab分析:aba//ba//abb如图:已知直线,,平面,且,,,都在平面外。求证://abcac证明:过作面交于a//aca//ca//bb//ccbb//线线////线线线线////面面转化是立体几何的一种重要的思想方法说明:证明:P62习题5已知:如图,AB//平面,AC//BD,且AC、BD与分别相交于点C,D.求证:AC=BDAC//BDACBD与确定一个平面ADAB//平面ADCD平面平面ADAB平面//ABCD//ACBDABCD为平行四边形ACBD练习要证,通过要证,通过构造构造过直线过直线aa的平面与平面的平面与平面相交于直线相交于直线bb,,只要证得只要证得a//ba//b即可。即可。//a小结小结证明线面平行的证明线面平行的转化思想:转化思想:线线////线线线线////面面面面////面面(1)(1)平行公理平行公理(2)(2)三角形中位线三角形中位线(3)(3)平行线分线段成比例平行线分线段成比例(4)(4)相似三角形对应边成比例相似三角形对应边成比例(5)(5)平行四边形对边平行平行四边形对边平行练习练习四、课堂练习:(1)以下命题(其中a,b表示直线,表示平面)①若a∥b,b,则a∥②若a∥,b∥,则a∥b③若a∥b,b∥,则a∥④若a∥,b,则a∥b其中正确命题的个数是()(A)0个(B)1个(C)2个(D)3个判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.(1)如果a、b是两条直线,且ab,∥那么a平行于经过b的任何平面;()(2)过平面外一点和这个平面平行的直线只有一条.()填空:(2)若两直线a、b相交,且a∥α,则b与α的位置关系可能是b∥α,b与α相交b∥α或bα,或b与α相交(1)若两直线a、b异面,且a∥α,则b与α的位置关系可能是2.判断下列命题的真假(1)过直线外一点只能引一条直线与这条直线平行.()(2)过平面外一点只能引一条直线与这个平面平行.()(3)若两条直线都和第三条直线垂直,则这两条直线平行.()(4)若两条直线都和第三条直线平行,则这两条直线平行.()真假真假作业:P62T5、T6再见!例例33::ABCDMNNBCPCMBAPABBBBPDCBAABCD平面求证:)、(异于中,点-长方体//,,11111111分析分析证法证法11ABA1DB1D1PCC1MN证法证法22例例33:证:证ABA1DB1D1PCC1MN明明111111111111////CACACAACACCACCAACAAC面面长方体中、连结MNBCAACPNBCPCMPABAACPACBCAAC111111//面面面面ABCDACABCDMNMNAC面面//ABCDMN面//证法证法11的思路是的思路是线线////线线线线////面面线线////线线线线////面面证法证法22利用相似三角形对应边成比例利用相似三角形对应边成比例及平行线分线段成比例的性质及平行线分线段成比例的性质111111AACCCCPBNCPNNCCPBNAAPBMAPMMAAPBM∽∽NCPNMAPM∽∽(略写)(略写)ABCDACABCDMNMNAC面面//ABCDMN面//ABA1DB1D1PCC1MN证法证法11