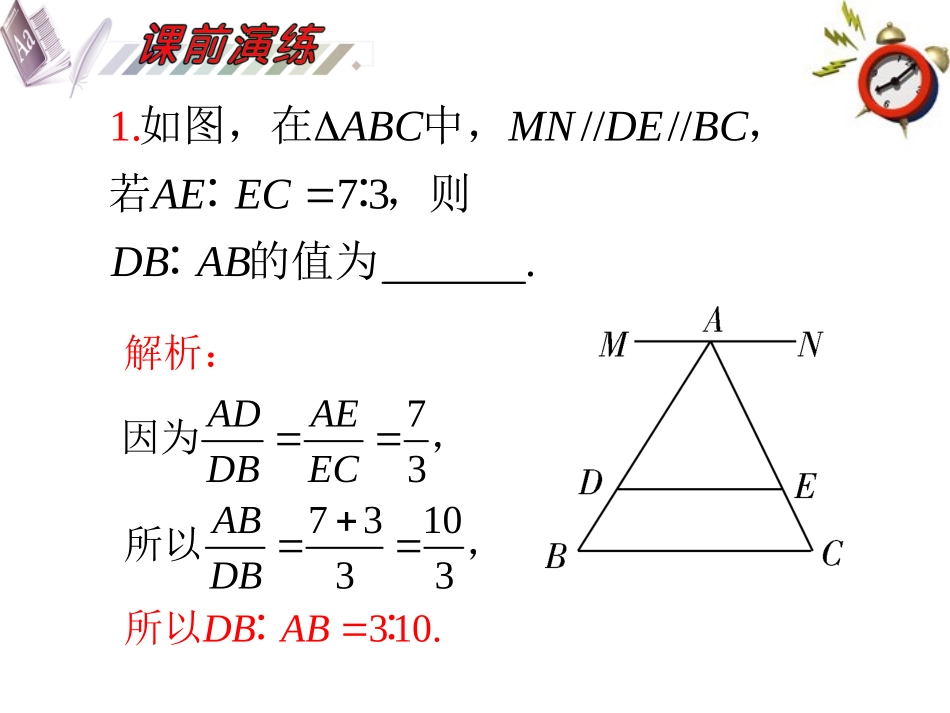
123.理解相似三角形的定义,掌握相似三角形的三个判定定理的证明方法..了解平行线分线段成比例定理..理解并掌握直角三角形射影定理.////73.1.ABCMNDEBCAEECDBAB如图,在中,,若∶∶,则∶的值为3737131033.0ADAEDBECABDBABBD解析:所因为,,以∶∶所以49.2.两个相似三角形的周长分别是和,则两个三角形的面积比是111111121416().891SaSabcabcabcacab解,所以因为析:3.CDABC如图,是直角三角形斜边上的高,则图中相似的三角形有对.3..4ADBCBCEADBECE如图,已知点、在直线上的射影分别为、,点为线段的中点,则与的大小关系为BECE/.///.EEFBCFABEFCDEADBEFBCEFBCCE过点作于,则因为为的中点,所以为的中点,所以是的中垂线,解析:则-.5ABCDABaBCbCCEBDEBE在矩形中,,,过作于,则22222.BCBCBEBDbBEBDab由直角三角形解析:所以射影定理可知,//436..DEBCBFEFACAE如图,已知,且∶∶,则∶//434.//3.DEBCDEFCBFBFEFBCACAEBCDEDEDEBCADEABC因为,所以∽,所以∶∶∶又解析:所以∶∶因为,所以∶∽,1__________.21__________3_________1_x定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也①推论:经过三角形一边的中点与另一边平行的直线必②第三边.经过梯形一腰.平行线等分线段定理的中点,且与底边平行的直线③另一腰.__________()____________________2_3_____三条平行线截任意两条直线,所截出的④成比例.推论:平行于三角形一边的直线截其他两边或两边的延长线,所得的⑤成比例.对应角⑥,对.平行线分线段成比例定理及推论.相似三角形应边⑦的两个三角形叫做两个相似的定义三角形.1__________2____________3_______1________.2________.3___45_____判定定理:两角对应⑧的两个三角形相似.判定定理:两边对应⑨,并且夹角⑩的两个三角形相似.判定定理:三边对应的两个三角形相似.相似三角形对应边上的高、中线和对应角平分线的比都等于相似三角形周长的比等于相似三角形的面积比等于.相似三角形的判定.相似三角形的性质_____._________.6直角三角形中,每一条直角边是这条直角边在斜边上的射影和斜边的;斜边上的高是两条直角边在斜边上的射影的.直角三角形射理影定【要点指南】////69__1.______.ABEFCDABcmCDcmEF如图,已知,若,,则例题型一相似三角形的判定与性质//18..//.11659EFCFABCEFABABCBEFBFDBCEFCDCDBCEFEFCFBFABCDCBEFBCEmEFcF在中,因为,所以在中,因解为,所以两式相加,得,所,故以析:-////.BCABCDBCABEFCDEF分由于是与的公共边,且,利用平行线分三角形成相似三角形可求析:11.1ABCDEF由证明过程我们发现,本题可以有以下一般结论:评析:____1.ABCDOOEBCEABFABaBCbBFcBE如右图,平行四边形的对角线交于点,交于,交的延长线于,若,,,则素材:”//“ABBCBFOOGBCABGBEFGOF本题所给出的已知线段、、位置分散,应设法利用平行四边形的等量关系,通过作辅助线将长度已知的线段集中到一个可解的图形中来.为此,过作,交于,分析:构造∽求解.//112211..12//2222OOGBCABGOGABCOGBCbGBABaGOFFBcbbcBEOGBEFBBEFGOFGOFBEGOaaGFGcc过作,交于,显然是的中位线,所以,在中,,所以∽,即所以,解析:解决平面几何问题时,当条件较分散时,可适当添作辅助线,使得分散的条件适评析:当集中.2//45.2..ABCDADBCACBDEABCEADADFBCGEADABHFGAFDFBGCGAHBH已知,如图,在梯形中,,,垂足为,,过作的垂线交于,交于,过作的平行线交于求证:例题型二直角三角形射影定理及应用22.ACBDAEDBECEFADEGBCAFDFEFBGCGEG因为,故、都是直角三角形.又,,由射影定理可知,解析:22AFDFEFBGCGEGFGFEEGEFEGAHBH由射影定理可知,,故考虑将,然后只需寻分析找:与的关系.222222245222..2FGFEEGFEEGFEEGAFDFBGCGFEEGABCAHBCAHFEBHEGFGAFDFBGCGFEEGAFDFBAHBHEFEGGCG...