高考数学一轮复习课件：11.2直线的方程 课件VIP免费

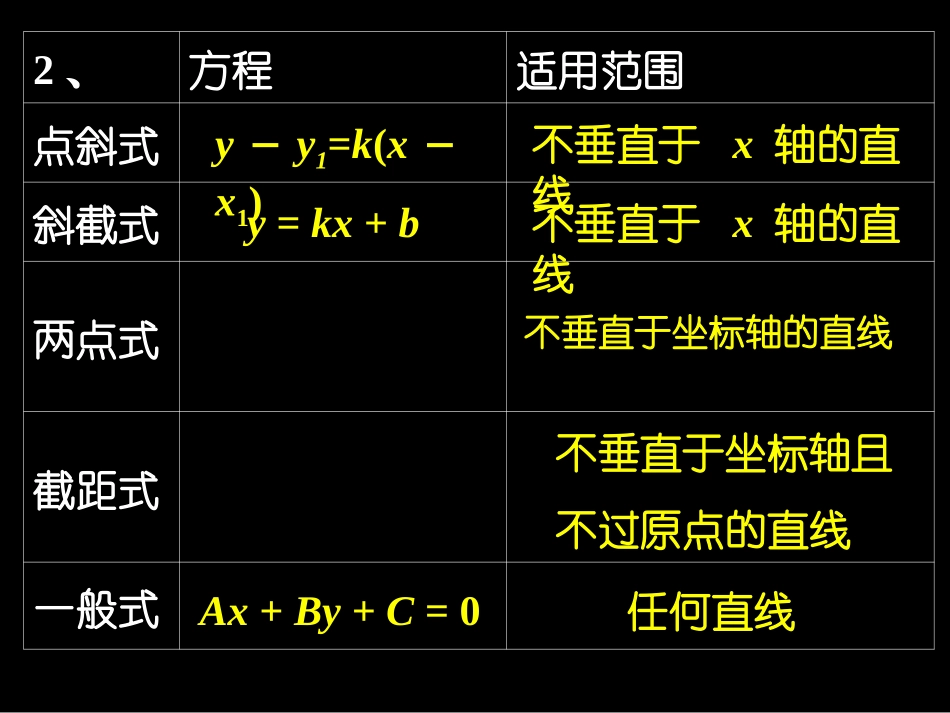
基础知识：1、两点距离公式：|P1P2|=_______________221221)()(yyxx2、方程适用范围点斜式斜截式两点式截距式一般式y－y1=k(x－x1)y=kx+b不垂直于x轴的直线不垂直于x轴的直线不垂直于坐标轴的直线不垂直于坐标轴且不过原点的直线任何直线Ax+By+C=0121121xxxxyyyy1byax1、下面命题中正确的是（）（1）经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示.（2）经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示（3）不经过原点的直线都可以用方程1byax表示（4）经过点A(0,b)的直线都可以用方程y=kx+b表示（5）经过点(,2),(,1)PaQb的直线的斜率1kab5、以下四个命题:(1)所有直线总可以用直线的点斜式、斜截式表示;(2)直线的点斜式和斜截式是可以等价转换的;(3)一次函数的图象是一条直线,直线方程总可以用一个一次函数去表示;(4)斜截式y=kx+b中的b表示直线与y轴交点到原点的距离.其中正确命题的题号是____2、经过点(2,1)，且斜率为3的直线l的点斜式方程为，斜截式方程经过两点(-1,8)和点(4,2)的直线l的两点式方程为截距式方程为一般式方程为3、过点A(2,1),且在x,y轴上截距相等的直线方程是6、过点(5,2),且在x轴上的截距是在y轴上的截距的2倍的直线方程是4、一直线过点A（－3，4），且在两轴上的截距之和为12，则此直线方程是。例2:已知直线l与两坐标轴围成的三角形面积为3，分别求满足下列条件的直线方程：1(1)(3,4);(2)6A过点斜率为练习：(2,1),(1,2)lAll直线经过点且点到直线距离为1,求直线方程变式：已知直线1：y=4x与点P（6，4），在1上求一点Q，使直线PQ与直线1，以及x轴在第一象限围成的三角形面积最小．变式：已知直线l：y=4x与点P(6,4),在l上求一点Q，使直线PQ与直线l，以及x轴在第一象限围成的三角形面积最小练习：1、求满足下列条件的直线l的方程新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆⑴在y轴上的截距为3，且它与两坐标轴围成的三角形面积为6；⑵与直线240xy的夹角为045，且交点在x轴上新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆例题3、设过点P(2,1)作直线l交x轴的正半轴、y轴的正半轴于A、B两点，（1）当取得最小值时，求直线l的方程．（2）当取得最小值时，求直线l的方程．||||PAPB||||PAPBPAPBOAOB2、（选做题）一条直线经过点P（3，2），并且分别满足下列条件，求直线方程：1）倾斜角是直线x－4y+3=0的倾斜角的2倍；2）与x、y轴的正半轴交于A、B两点，且△AOB的面积最小（O为坐标原点）4.234ll例已知直线过点（，），且与坐标轴围成的三角形的面积为，求直线的方程。解：由题意知直线l与两坐标轴不垂直。).2(3xky设直线方程为,0x令;32ky得,0y令.32kx得于是直线与两坐标轴围成的三角形面积为.4323221kk8|1294|kkx0yP,83232kk若,09442kk整理得无解。,83232kk若,092042kk整理得.2921kk或解得.01229042yxyx或所求直线方程为：4.234ll例已知直线过点（，），且与坐标轴围成的三角形的面积为，求直线的方程。8|1294|kkx0yP方程及相应的最小值在两坐标轴上截距之和）（方程；最小值及相应的直线）求（两点，、相交于正半轴、且与过点、直线例lllSBAyxPlOAB21)1,4(5x0y)1,4(PAB)0,0(),,0(),0,(1babBaA）设解（1byax则直线方程为)1,4(Pl过点直线114baabab4abab442821abS16ab时取等号）即（当2,84baba084128,8minyxyxlS方程为直线方程及相应的最小值在两坐标轴上截距之和）（方程；最小值及相应的直线）求（两点，、相交于正半轴、且与过点、直线例lllSBAyxPlOAB21)1,4(5x0y)1,4(PAB)0,0(),,0(),0,(2babBaA）设解（1byax则直线...