福建省建瓯市高一数学(平面与平面垂直的判定)课件VIP免费

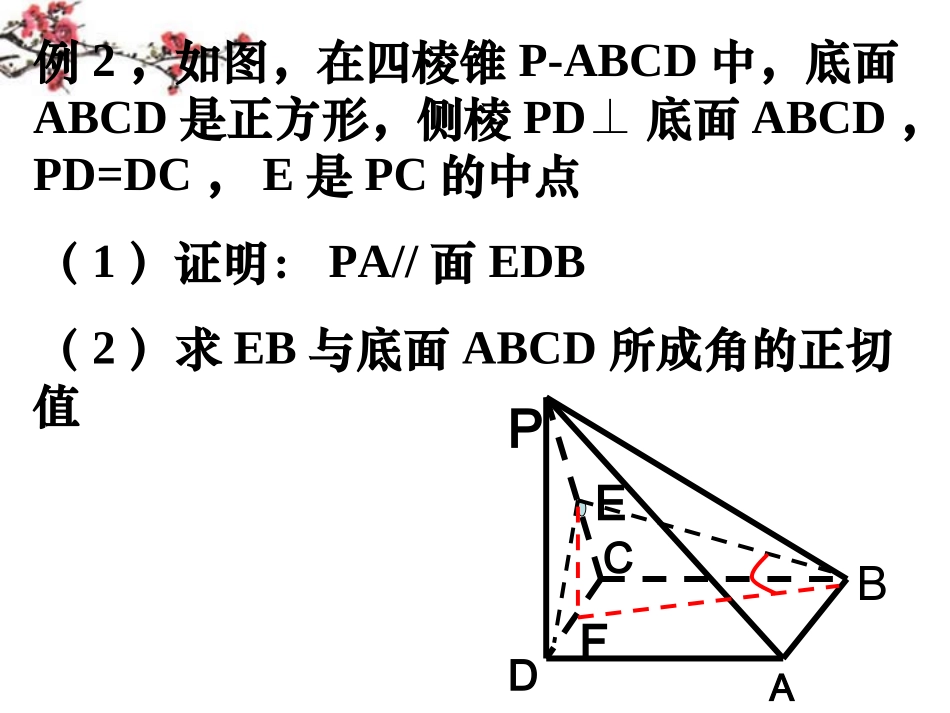
如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面。1.线面垂直的判定定理平面的一条斜线和它在这个平面内的射影所成的夹角，叫做斜线和平面所成的角(或斜线和平面的夹角).简称线面角2.斜线和平面所成的角3.直线与平面所成的角θ的取值范围是：斜线与平面所成的角θ的取值范围是：2020温故知新例2，如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点（1）证明：PA//面EDB（2）求EB与底面ABCD所成角的正切值PDCABEF练习，如图，已知SARTABC⊥⊿所在平面，BCAC⊥，∠ABC=30°，AC=1，SB=2√3，求SC与面SAB所成角的正弦值。._____,,,).3._____,).2.__,90,).1.,,,,,.20心的是则若心的是则若点边的是则若连接为垂足作外一点所在平面过ABCOPAPCPCPBPBPAABCOPCPBPAABOCPCPBPAPCPBPAOPOPABC深度探究深度探究::中外垂思考1:平面上的一条直线将平面分割成两部分，每一部分叫什么名称？半平面半平面一、二面角的定义思考2:将一条直线沿直线上一点折起，得到的平面图形是一个角，将一个平面沿平面上的一条直线折起，得到的空间图形称为二面角，你能画一个二面角的直观图吗？一、二面角的定义二面角•∠AOB即为二面角α-AB-β的平面角的平面角从一条直线出发的两个半平面所组成的图形注意：lOAB以二面角的棱上任一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角二面角的平面角的三个特征:平面角是直角的二面角叫做直二面角(1)顶点在棱上；(2)边在两个面内；(3)边垂直于棱.B1C1D1A1ABCDMN寻找平面角寻找平面角CABSDD端点端点中点中点寻找平面角寻找平面角中点中点B1C1D1A1ABCDMNEEGGFF练习1、已知正三棱锥V-ABC所有的棱长均相等，找二面角A-VC-B的平面角。VABCBDCAS2.如图，正四棱锥S-ABCD中，SA=SB=SC=SD=4,AB=BC=CD=DA=2,找侧面与底面所成的二面角？一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.面面垂直的定义：(2)日常生活中平面与平面垂直的例子?(1)除了定义之外,如何判定两个平面互相垂直呢?αβaAb平面与平面垂直的判定定理一个平面过另一个平面的垂线，则这两个平面垂直.符号:αβaA简记：线面垂直，则面面垂直面面垂直线面垂直线线垂直aa面符号:例:如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A,B的任意一点，求证：PACPBC.平面平面PABCO典例剖析证明:设已知⊙O平面为α,PABC面面BCPA为圆的直径又ABBCACPAACABCPAC面PACPBC面面BCPBC面PABCACBCPAPACACPAC面面2.正方体ABCD-A1B1C1D1中求证:111AACCABD面面证明:1AAABCD面ABCDBD面又1AABDBDAC1ACAAA且11BDAACC面1BDABD面111AACCABD面面ACBDA1C1B1D1课堂练习课堂练习1.空间四面体ABCD中，若AB=BC，AD=CD，E为AC的中点，则有（）ABCED(A)平面ABD⊥面BCD(B)平面BCD⊥面ABC(C)平面ACD⊥面ABC(D)平面ACD⊥面BDE探究1：ACBDA1C1B1D1如图为正方体,请问哪些平面与垂直?1ABAC面面11BCBA面面111CABA面面11ADBA面面面面垂直线面垂直线线垂直1AB面探究1：ACBDA1C1B1D1111111111111111BCBCBCABBCABBBCABCDABABCD平面平面1111ABCDABCD平面平面11ABCD1BC平面111BCABCD平面探究1：ACBDA1C1B1D1探究1：ACBDA1C1B1D1探究1：ACBDA1C1B1D1,ABBCDBCCD已知面请问哪些平面互相垂直的,为什么?ABCBCD面面ABCACD面面ABDBCD面面ABBCD面CDABC面ABBCD面探究2：ABCD1、证明面面垂直的方法：（1）证明二面角为直角（2）用面面垂直的判定定理2、面面垂直线面垂直线线垂直学完一节课或一个内容，学完一节课或一个内容，应当及时应当及时小结小结，梳理知识，梳理知识作业•A：小结•B：P81A3•C：小结二面角及其平面角线面垂直判定定理：mαnαm∩n=Bl⊥ml⊥nl⊥αAmnlB