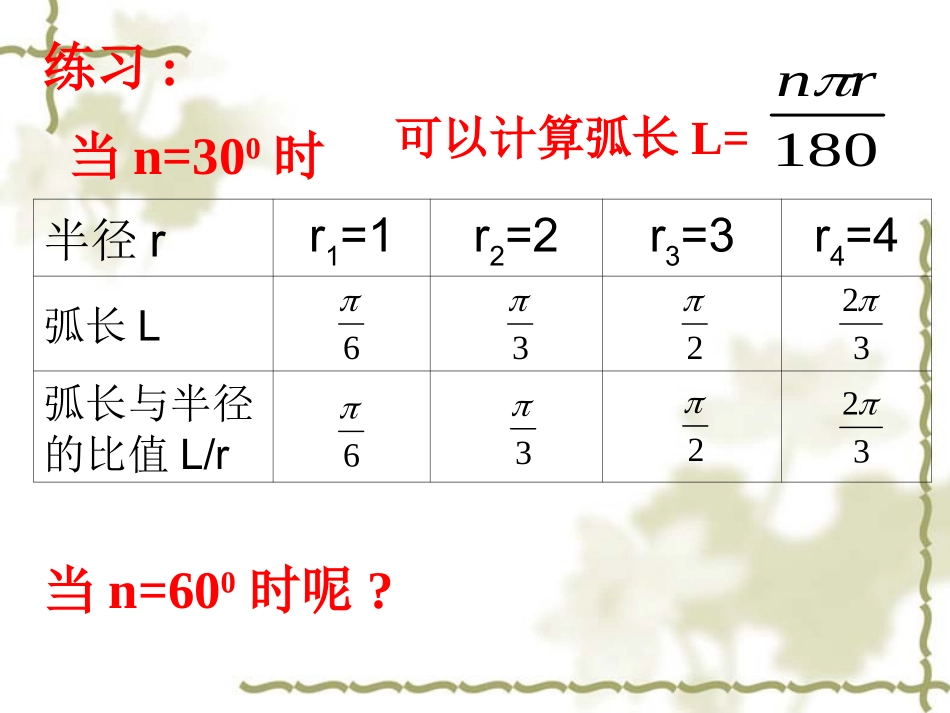
弧度制知识回顾1、角度制的定义规定周角的1/360为1度的角,这种用度做单位来度量角的制度叫角度制。可以计算弧长L=180rn60°090°0半径rr1=1r2=2r3=3r4=4弧长L弧长与半径的比值L/r当n=300时练习:当n=600时呢?可以计算弧长L=180rn66322332321、1弧度角的定义我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。1弧度rL=rOAB设弧AB的长为L,若L=r,则∠AOB=1弧度Lr=若L=2r,则∠AOB=2弧度若L=2πr,则∠AOB=2π弧度Lr=2弧度rOABL=2r2π弧度L=2πrOA(B)rLr=若圆心角∠AOB表示一个负角,且它所对的弧的长为3r,则∠AOB的弧度数的绝对值是Lr=3,即∠AOB=-Lr=-3弧度L=3rOABr-3弧度2.一般地,我们规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,任一已知角α的弧度数的绝对值:︱α︱=Lr其中L为以角α作为圆心角时所对圆弧的长,r为圆的半径。这种用“弧度”做单位来度量角的制度叫做弧度制。由弧度的定义可知:圆心角AOB的弧度数等于它所对的弧的长与半径长的比的绝对值。定义的合理性1弧度rL=rOAB1弧度rL=rOAB与半径长无关的一个比值3、弧度与角度的换算L=2πrOA(B)2π弧度rLr=若L=2πr,则∠AOB=2π弧度此角为周角即为360°360°=2π弧度180°=π弧度由180°=π弧度还可得1°=——弧度≈0.01745弧度180π1弧度=(——)°≈57.30°=57°18′π1804、例1(1)、把67°30′化成弧度。(2)、把—π弧度化成度。53例2.把下列各角化成弧度(1)67°30',(2)120°,(3)75°,(4)135°(5)300°,(6)-210°,(7)22°30',(8)225°例3.把下列各弧度化成度.(1)3π/5,(2)π/12,(3)3π/10,(4)–π/5(5)-12π,(6)5π/6,(7)7π/12例4:已知扇形AOB的周长是8cm,该扇形的中心角是2rad。求该扇形的面积。注:1、对于一些特殊角的度数与弧度数之间的换算要熟记。度0°30°45°60°90°180°270°360°弧度062323422、用弧度为单位表示角的大小时,“弧度”二字通常省略不写,但用“度”(°)为单位时不能省。3、用弧度为单位表示角时,通常写成“多少π”的形式。4、用弧度来度量角,实际上角的集合与实数集R之间建立一一对应的关系:实数集R角的集合正角零角负角正实数零负实数对应角的弧度数练习:P111、2、3、4小结:2、量角的制度,除了角度制与弧度制以外,还有其它的制度,弧度制除了使角与实数有一一对应关系外,为以后学习三角函数打下基础。3、能熟练地进行角度与弧度之间的换算。1.圆心角α所对弧长与半径的比是一个仅与角α大小有关的常数,所以作为度量角的标准.