高中数学空间向量运算的坐标公式课件VIP免费

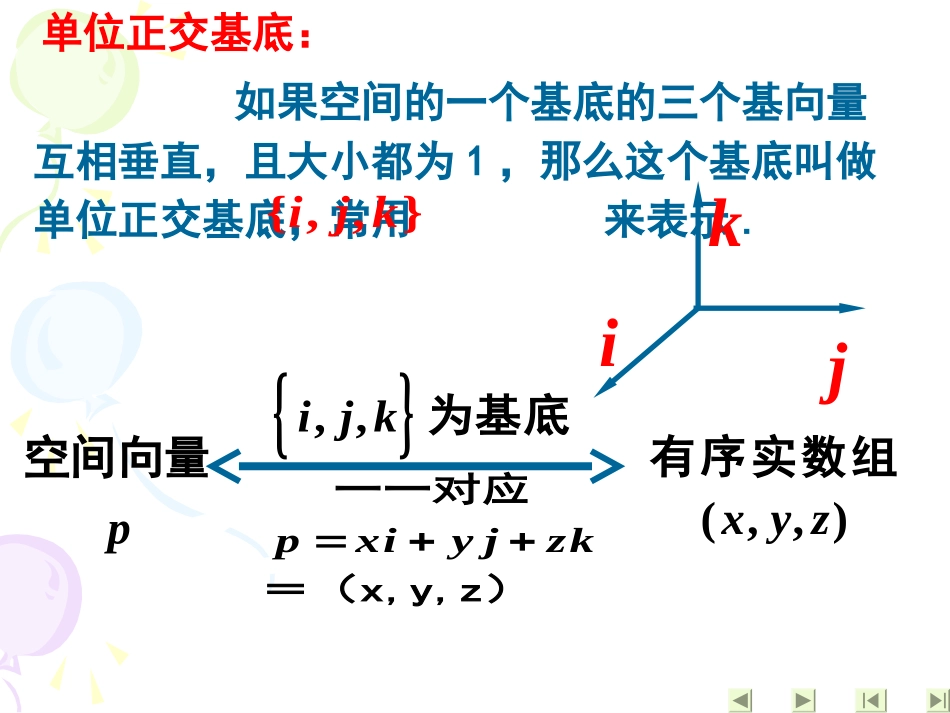
空间向量运算的坐标公式空间向量运算的坐标公式复习：空间向量的基本定理：如果三个向量不共面，那么对空间任一向量，存在一个唯一的有序实数组x、y、z，使得：c,b,apczbyaxpcba,,叫做空间的一个______基底空间任意三个不共面向量都可以构成空间的一个基底单位正交基底：如果空间的一个基底的三个基向量互相垂直，且大小都为1，那么这个基底叫做单位正交基底，常用来表示.{,,}ijk��ik�j有序实数组(,,)xyz一一对应pxiyjzk�＝（x,y,z）,,ijk��为基底空间向量p�新课讲解：向量的直角坐标运算.111222(,,),(,,)axyzbxyz设则121212(,,);abxxyyzz111(,,)();axyzR121212;abxxyyzz121212(,,);abxxyyzz例1、（1）求向量(,,)axyz的模||a（2）求两个非零向量111(,,)axyz，222(,,)bxyz的夹角的余弦值练习1.知(2,3,5)a，(3,1,4)b，求ab，ab，||a，8a，ab，练习1-2、已知(,2,2)ax，(2,3,5)b，且a与b的夹角为钝角，求x的取值范围；练习1：练习1-3、已知(1,1,)attt，(2,,).btt。||ba求的最小值。例2、（1）已知向量(2,3,5)a，(3,1,)bz，且ab，求Z的值。（2）求两个非零向量111(,,)axyz，222(,,)bxyz若//ab则有。练习2练习2-1、已知(cos,1,sin)aaa，(sin,1,cos)baa，则向量ab与ab的夹角为练习2-2、已知(sin,cos,tan)aaaa，(cos,sin,cot)baaa且ab，则a角＝练习2-3、已知向量(2,-1,3)a，求向量b，使得//ab，且||3||ba＝课堂小结：空间向量的坐标运算公式、模长公式、夹角公式及其应用。注：空间向量的坐标运算公式、模长公式、夹角公式的形式与平面向量中相关内容一致，因此可类比记忆；