高中数学 正弦定理课件 苏教版必修5 课件VIP免费

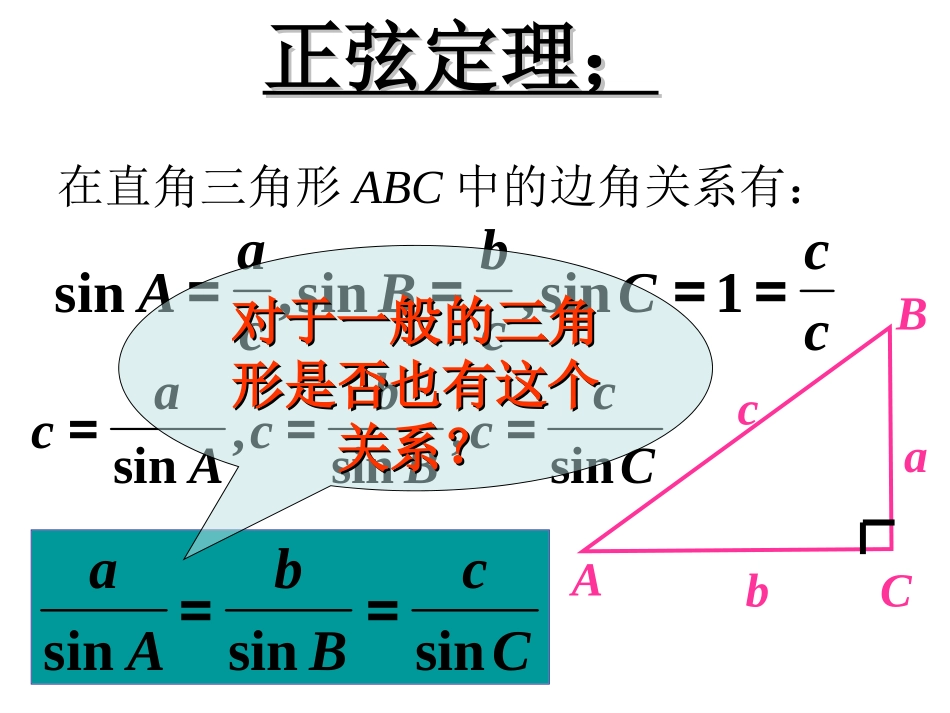
正弦定理正弦定理；正弦定理；ABCabc在直角三角形ABC中的边角关系有：ccCcbBcaA====1sin,sin,sinCccBbcAacsin,sin,sin===CcBbAasinsinsin==对于一般的三角对于一般的三角形是否也有这个形是否也有这个关系？关系？证明一:在任意斜△ABC当中：S△ABC=两边同除以即得：==AbcBacCabsin21sin21sin21abc21AasinBbsinCcsinCcBbAasinsinsin==证法二:∵边AB、AC在y轴上射影相等,∴bsinC＝csinB,＝bsinBcsinC∴.同理＝.asinAbsinB＝＝.asinAbsinBcsinC∴ABCabcxyxyABCabc在一个三角形中各边和它所对角的正弦的比相等.＝＝asinAbsinBcsinC＝正弦定理？＝＝asinAbsinBcsinC＝2R.=2RbsinBB`ABCbOABCbOB`ABCbO（1）已知两角及一边；（2）已知两边和其中一边的对角；（3）已知两边及夹角；（用余弦定理）（4）已知三边.（用余弦定理）ABCabc＝＝asinAbsinBcsinC＝2R.例1在ABC中，已知c＝10，A＝45°，C＝30°，求b.解：∵＝，bsinBcsinCB=180°–(A＋C)＝105°，ABCcbb＝≈19.csinBsinC∴注:这是一类已知两角和任一边,求其他两边和一角问题例2在ABC中，已知a＝20，b＝28，A＝40°，求B和c.解：∵sinB＝≈0.8999bsinAa∴B1＝64°，B2＝116°40°ABCbB1B2······注:这是一类已知两边的其中一边的对角解三角形的问题在例2中，将已知条件改为以下几种情况，结果如何？（1）b＝20，A＝60°，a＝20√3;（2）b＝20，A＝60°，a＝10√3;（3）b＝20，A＝60°，a＝15.60°ABCb（1）b＝20，A＝60°，a＝20√3sinB＝＝，bsinAa12B＝30°或150°，∵150°＋60°>180°，∴B＝150°应舍去.60°2020√3ABC（2）b＝20，A＝60°，a＝10√3sinB＝＝1，bsinAaB＝90°.B60°AC20（3）b＝20，A＝60°，a＝15.sinB＝＝，bsinAa2√332√33∵>1，∴无解.60°20AC思考：当b＝20，A＝60°，a＝？时，有1解、2解、无解.√230°练习ABC中，（1）已知c＝√3，A＝45°，B＝75°，则a＝____，（2）已知c＝2，A＝120°，a＝2√3，则B＝____，（3）已知c＝2，A＝45°，a＝，则B＝_____________.2√6375°或15°小结2.正弦定理可解以下两种类型的三角形：（1）已知两角及一边；(只有一解)（2）已知两边及其中一边的对角→↓.1.正弦定理是解斜三角形的工具之一.＝＝asinAbsinBcsinC＝2R解三角形时，注意大边对大角babababaa已知边a,b和A仅有一个解有两个解仅有一个解无解abCH=bsinA