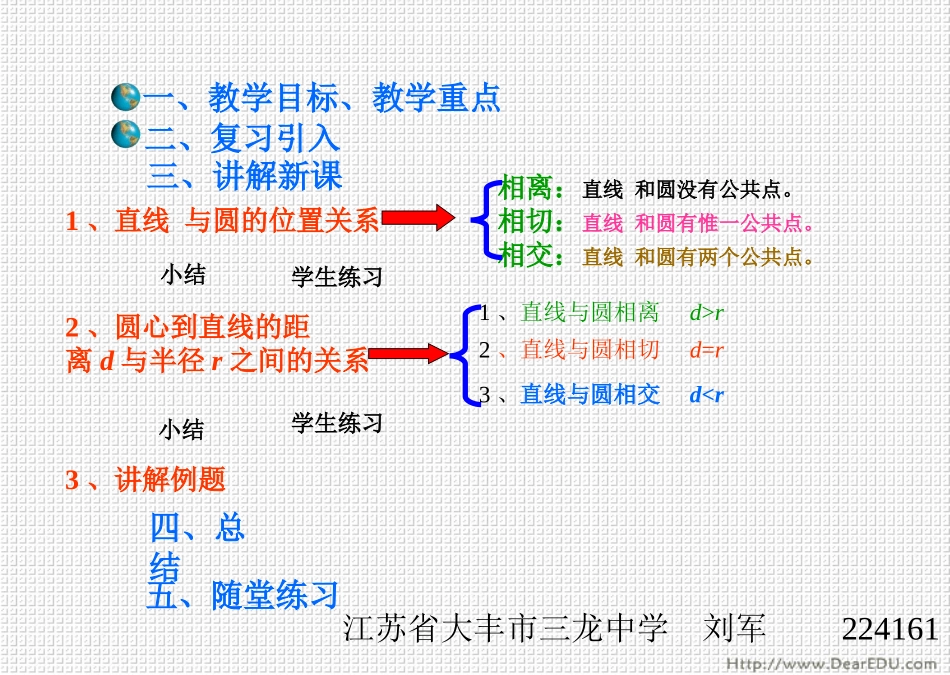
直线与圆的位置关系一、教学目标、教学重点二、复习引入三、讲解新课1、直线与圆的位置关系相离:直线和圆没有公共点。相切:直线和圆有惟一公共点。相交:直线和圆有两个公共点。小结学生练习2、圆心到直线的距离d与半径r之间的关系3、讲解例题四、总结五、随堂练习小结学生练习1、直线与圆相离d>r2、直线与圆相切d=r3、直线与圆相交dr2、直线与圆相切d=r3、直线与圆相交d”读作___________,它表示两个方面:(1)“=>”即从____端可以推出___端(反映直线与圆的某种位置关系的性质)(2)“<=”即从____端可以推出___端(反映直线与圆的某种位置关系的判定)等价于左右右左3、直线与圆相交<=>dd>r2、直线与圆相切<=>d=r直线与圆的位置关系直线与圆的位置关系相交相切相离公共点个数公共点名称直线名称圆心到直线距离d与半径r的关系dr2交点割线1切点切线0总结:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________的个数来判断;(2)根据性质,由_______________________________的关系来判断。在实际应用中,常采用第二种方法判定。两直线与圆的公共点圆心到直线的距离d与半径r练习2填空:1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是___。动动脑筋相交相切两个3、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是___。零相离思考:圆心A到X轴、Y轴的距离各是多少?例题1.AOXY已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切例题2讲解在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm(2)r=2.4cm(3)r=3cmBCA分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB===5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD===2.4(cm)。2222D4532.4cm2.4cm思考:图中线段AB的长度为多少?怎样求圆心C到直线AB的距离?即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, d>r,∴⊙C与AB相离...