高三数学 8.5椭圆的定义与标准方程复习课件VIP免费

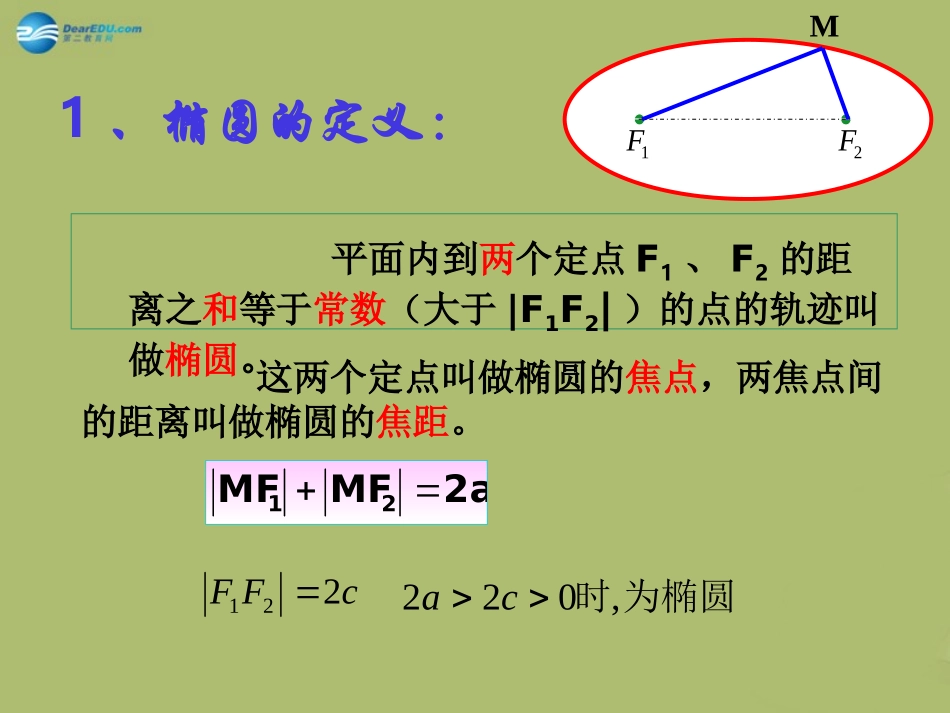
10．函数,),(Dxxfy若存在常数C，对任意的,1Dx存在唯一的Dx2使得,)()(21Cxfxf则称函数)(xf在D上的几何平均数为C．已知],2,1[,)(3xxxf则函数3)(xxf在[1,2]上的几何平均数为A．2B．2C．4D．22()2xfx变式：D一轮复习讲义一轮复习讲义椭圆1、椭圆的定义：1F2FM平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。cFF221为椭圆时,022ca2aMFMF211．椭圆的概念定义：在平面内到两个定点F1、F2的距离的和等于常数(大于F1F2)的点的轨迹叫做．这两定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的．集合P＝{M|MF1＋MF2＝2a}，F1F2＝2c，其中a>0，c>0，且a，c为常数：①若，则集合P为椭圆；②若，则集合P为线段；③若，则集合P为空集．忆一忆知识要点椭圆焦距a>ca＝cab>0)y2a2＋x2b2＝1(a>b>0)图形忆一忆知识要点范围－a≤x≤a－b≤y≤b－b≤x≤b－a≤y≤a对称性对称轴：坐标轴对称中心：原点顶点A1(－a,0)，A2(a,0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)B1(－b,0)，B2(b,0)轴长轴A1A2的长为2a；短轴B1B2的长为2b焦距F1F2＝2c离心率性质a，b，c的关系c2＝a2－b22．椭圆的标准方程和几何性质e=(0,1)ac题型一.椭圆的定义1.下列说法中，正确的是（）A．平面内与两个定点1F，2F的距离和等于常数的点的轨迹是椭圆B．与两个定点1F，2F的距离和等于常数（大于12FF）的点的轨迹是椭圆C．方程2222210xyacaac表示焦点在x轴上的椭圆D．方程222210,0xyabab表示焦点在y轴上的椭圆C2.1F，2F是定点，126FF，动点M满足126MFMF，则点M的轨迹是（）A．椭圆B．直线C．线段D．圆3.若方程22135xykk表示椭圆，则k的取值范围为________________.C3,44,5自测3，1（4）例1.一动圆与已知圆O1：(x＋3)2＋y2＝1外切，与圆O2：(x－3)2＋y2＝81内切，试求动圆圆心的轨迹方程．利用椭圆的定义求轨迹方程：O1PMxyoO2变式迁移1求过点A(2,0)且与圆x2＋4x＋y2－32＝0内切的圆的圆心的轨迹方程．O1PMxyoO2题型二．椭圆的标准方程例2.(1)椭圆以坐标轴为对称轴,且长轴是短轴的3倍,且过点A(3,0),求椭圆方程;(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点A(0,2),B(1,2,3),求椭圆的方程.3.已知P点在焦点在x轴的椭圆上，点P到两焦点的距离分别为5和3，过P作长轴的垂线恰好过椭圆的一个焦点，求此椭圆的方程．【变式2】求适合下列条件的椭圆的标准方程：(1)已知椭圆过（3,0），离心率e=63,求椭圆的标准方程；(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P1(6,1),P2(-3,-2),求椭圆的方程.变式训练12.已知圆(x＋2)2＋y2＝36的圆心为M，设A为圆上任一点，且点N(2,0)，线段AN的垂直平分线交MA于点P，则动点P的轨迹是()A．圆B．椭圆C．双曲线D．抛物线B当堂检测MNPAxyo