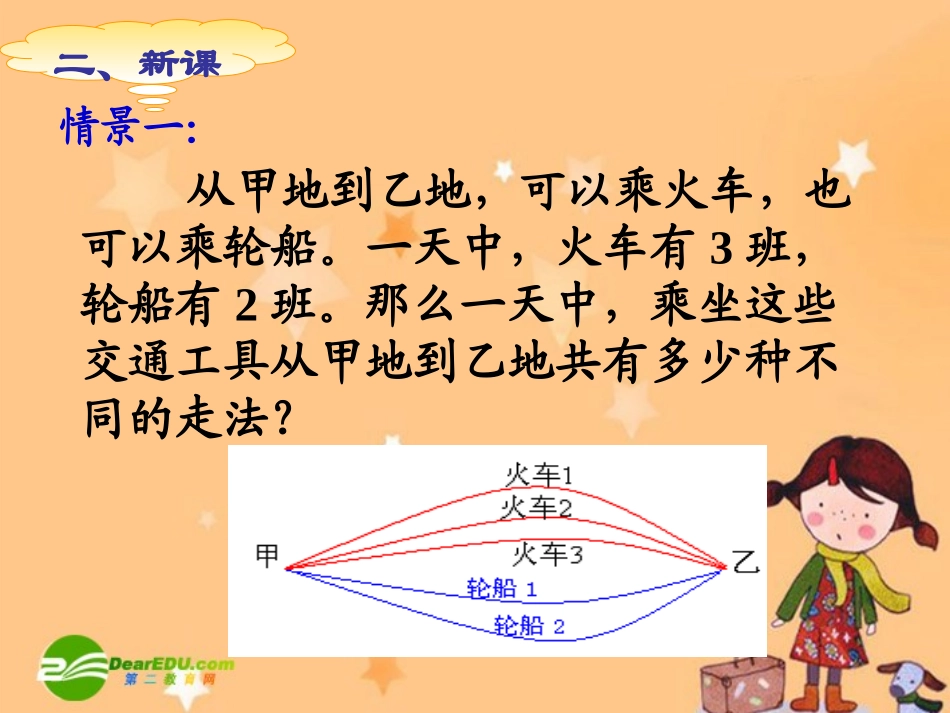
一学生从外面进入教室有多少种走法?若进来再出去,有多少走法?情景:一、导入分类计数原理和分步计数原理情景一:从甲地到乙地,可以乘火车,也可以乘轮船。一天中,火车有3班,轮船有2班。那么一天中,乘坐这些交通工具从甲地到乙地共有多少种不同的走法?二、新课分类计数原理分类计数原理做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法。那么完成这件事共有N=m1+m2+…+mn种不同的方法。(此原理又称加法原理)情景二:从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地乘汽车到乙地。一天中,火车有3班,汽车有2班,那么两天中,从甲地到乙地共有多少种不同走法?分步计数原理分步计数原理做一件事情,完成它需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事有N=m1×m2×…×mn种不同的方法。(此原理又称乘法原理)原理的共同点、区别:(小组讨论、原理的共同点、区别:(小组讨论、共同总结)共同总结)分类计数原理:方法相互独立,每种方法均能独立完成这件事分步计数原理:各步骤中的方法相互依存,只有各个步骤都完成才算完成这件事都是有关完成一件事情的不同方法的种数的问题。共同点共同点区别区别分类计数和分步计数原理剖析分类计数和分步计数原理剖析例1.书架放有3本不同的数学书,5本不同的语文书,6本不同的英语书。(1)若从这些书中任取1本书,有多少种不同的取法?(2)若从这些书中,取数学书、语文书、英语书各一本,有多少种不同的取法?(3)若从这些书中,取不同科目的书两本,有多少种不同的取法?解:(1)从书架上任取1本书,有3类办法:第1类办法是从3本不同的数学书中任取1本,有3种办法;第2类办法是从5本不同的语文书中任取1本,有5种办法;第3类办法是从6本不同的英语书中任取1本,有6种办法;根据分类计数原理,不同取法的种数是N=3+5+6=14答:从书架上任取1本书,有14种不同的取法。典型例题典型例题例1.书架放有3本不同的数学书,5本不同的语文书,6本不同的英语书。(1)若从这些书中任取1本书,有多少种不同的取法?(2)若从这些书中,取数学书、语文书、英语书各一本,有多少种不同的取法?(3)若从这些书中,取不同科目的书两本,有多少种不同的取法?解:(2)从书架上任取数学书、语文书、英语书各一本,需分成三个步骤完成:第1步取1本数学书,有3种办法;第2步取1本语文书,有5种办法;第3步取1本英语书,有6种办法;根据分步计数原理,不同取法的种数是N=3×5×6=90答:若从这些书中,取数学书、语文书、英语书各一本,有90种不同的取法。典型例题典型例题例1.书架放有3本不同的数学书,5本不同的语文书,6本不同的英语书。(1)若从这些书中任取1本书,有多少种不同的取法?(2)若从这些书中,取数学书、语文书、英语书各一本,有多少种不同的取法?(3)若从这些书中,取不同科目的书两本,有多少种不同的取法?解:(3)从书架取不同科目的书两本,有3类办法:第1类办法是数学书、语文书各取1本,有3×5种办法;第2类办法是数学书、英语书各取1本,有3×6种办法;第3类办法是语文书、英语书各取1本,有5×6种办法;根据分类计数原理,不同取法的种数是N=3×5+3×6+5×6=63答:若从这些书中,取不同科目的书两本,有63种不同的取法。典型例题典型例题例2:由1,2,3,4可组成多少个数字可以重复的四位数?变式1:由0,1,2,3可组成多少个数字可以重复的四位数?变式2:由1,2,3,4可组成多少个数字不可以重复的自然数?典型例题典型例题三、小结⑴通过本节课的学习,你学到了那些知识?⑵通过本节课的学习,你最大的体验是什么?⑶通过本节课的学习,你掌握了那些技能?四、作业1、课本P92、3、6。2、思考题:电子计算机的输入纸带每排有8个穿孔位置,每个穿孔位置可穿孔或不穿孔,则每排最多可产生多少种不同的信息?