高考数学复习 用垂线法做二面角资料 ppt 试题VIP免费

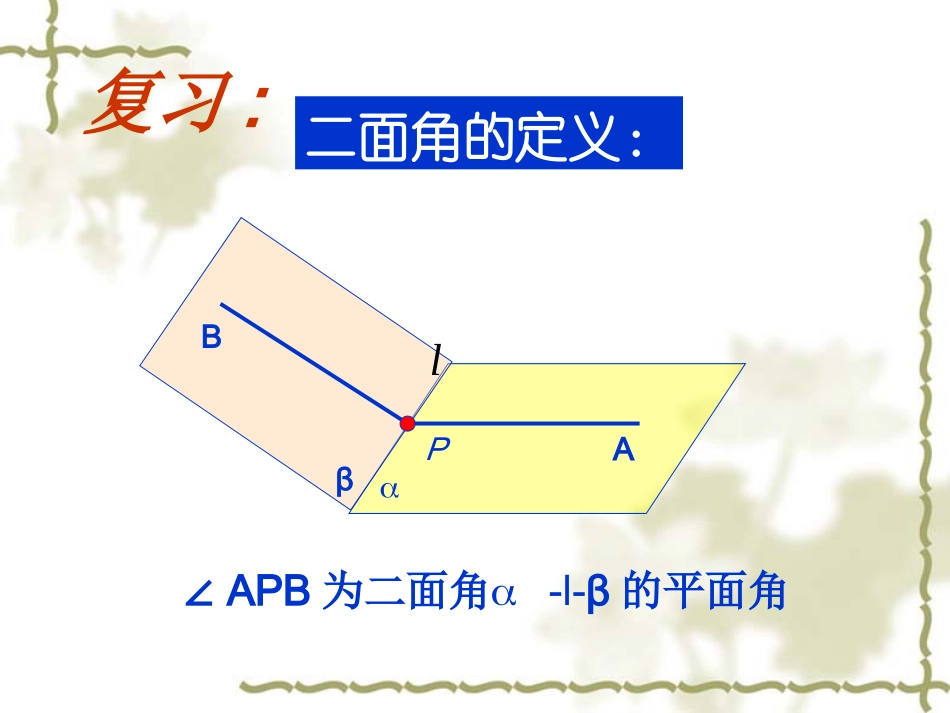
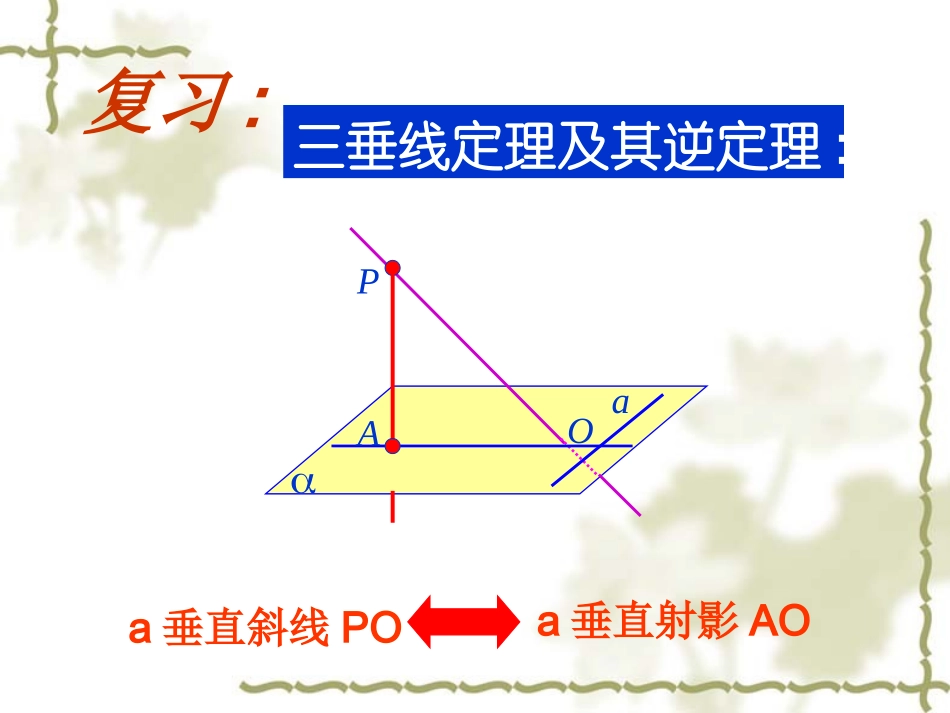
实验二中实验二中::李同刚李同刚βl复习:二面角的定义：AB∠APB为二面角-l-β的平面角P三垂线定理及其逆定理:复习:a垂直斜线POa垂直射影AOOPAa用三垂线定理求二面角的根据∴AO为斜线PO在的射影∵PA⊥平面若MNPO,⊥则MNOA⊥若MNOA,⊥则MNPO⊥∴∠POA为二面角-MN-β的一个平面角“撑柱子”我们把PO叫二面角的“撑柱子”求二面角的关键在于找:AOPMNβ例1:在正方体ABCD-C1B1A1D1中,试找出D1-AC-D的平面角,并求出它的正切.A1B1C1D1ABCDO撑柱子:DD1答案:tan∠DOD1=√2例2:NO已知在正方体ABCD-A1B1C1D1中，M为A1B上的点，且A1M=A1B,求二面角M－B1D1－A1的大小.13A1B1C1D1NO3√2答案:1A1B1C1D1ABCDMarctan2∠MON=例3:如图,P点为菱形ABCD所在平面外一点,∠ABC=60,PA=AC=a,PB=PD=a,点E在PD上,且PE:ED=2:1.(1)求证:PA⊥平面ABCD(2)以AC为棱,求面EAC与面DAC所成二面角.PABCDEaaaa证明:(1)∵菱形ABCD∠ABC=60∴AB=AC=a又∵PA=a,PB=a∴PA+AB=PB222∴PAAB⊥同理PAAD⊥∴PA⊥平面ABCDPABCDEaaaa过E点作EF⊥面ABCD,交AD与点F,过点F作DHAC,⊥交AC于H,连结EHFHADCFHFACDHEF=a/333aFH=RtEFH△中:∴tanEHF=∠33∴∠EHF=30度(2)C1A1DD1B1ABCE2341练一练:在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2,E是AB上的点,BE=1,求二面角C1-DE-C的正切值.如图:答案:tan∠C1FC=22F小结:1、找到或作出二面角的平面角(关键找撑柱子)2、证明1中的角就是所求的角3、计算出此角的大小一“作”二“证”三“计算”