高一数学平面的基本性质 新课标 课件VIP免费

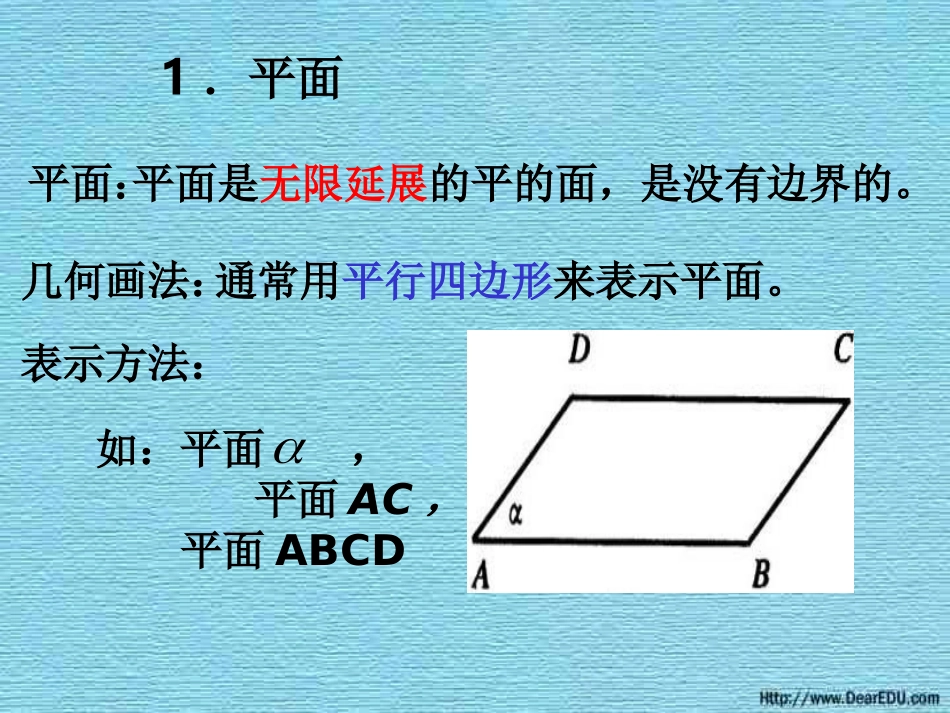
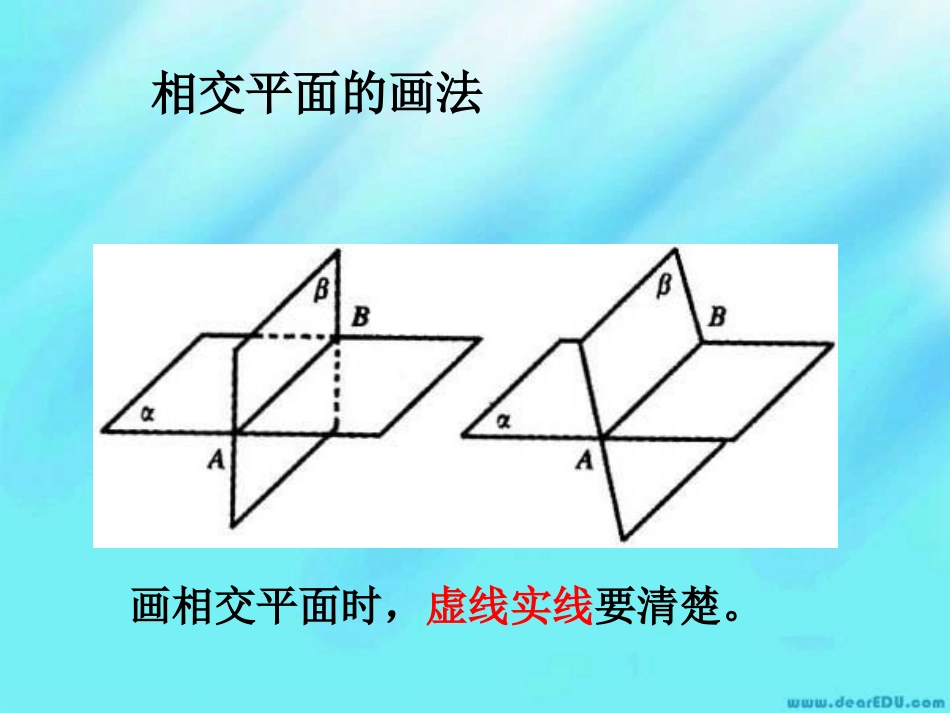
平面的基本性质1．平面平面：几何画法：平面是无限延展的平的面，是没有边界的。通常用平行四边形来表示平面。表示方法：如：平面，平面AC，平面ABCD相交平面的画法画相交平面时，虚线实线要清楚。点、线、面的位置关系（集合语言表示法）AB点Ｐ在直线l上，点Q不在直线l上，PQPlQl点A在平面内，点B在平面外，ll表示为：l直线a与b相交于点A,Aab表示为：Aba直线l在平面内,表示为：lA直线l在平面之外All(II)(I)表示为：//l,________)5(11BA________1BB________11BA练习,_______)1(1A_______1B,_______)2(1B_______1C,_______)3(1A_______1D正方体的各顶点如图所示，正方体的三个面所在平面，分别记作，试用适当的符号填空。1111,,ACABBC、、11_______)4(BA1_______BBAB桌面αAB平面的基本性质如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．公理1AB,ABAB直线判定直线在平面内的依据，同时说明了平面的无限延展性（直线是无限延展的）。公理1的作用ACBBCA经过不在同一条直线上的三点，有且只有一个平面。,,,,ABCABC三点不共线三点确定一平面公理2ACB公理2给出了确定一个平面的依据和方法。公理2的作用P天花板α墙面β墙面γ公理3如果不重合的两个平面有一个公共点，那么它们有且只有一条过这个点的公共直线．,PPlPl且说明两个不同平面相交于唯一一条交线，给出了确定平面交线的方法。公理3的作用直线不共面。（5）两两相交的三条则α与β重合。公共点，有三个不在一直线上的（4）平面α与平面βα.平面α，则a直线a，点A（3）若点A条直线确定一个平面。（2）经过同一点的三面。（1）三点确定一个平否正确：例1.判断下列命题是（×）（×）（×）（√）（×）例题。DB与平面ABC（2）平面AD；DD与平面BC（1）平面A两平面的交线：中，画出下列DCBD－A例2.在长方体ABC111111111111ABCDA1B1C1D1OABCDA1B1C1D1EF在同一平面上。l和l,求证：直线l且不过同一点，两两相交,l,l,例3.已知三条直线l321321αl3ACBl1l2例4、已知ΔABC在平面α外，AB、AC、BC的延长线分别与平面α交于点M、N、P三点，求证：M、N、P三点共线。αBACMNP小结公理1：判定直线在平面内的依据，同时说明了平面的无限延展性（直线是无限延展的）。公理2：给出了确定一个平面的依据。公理3：说明两个不同平面相交于唯一一条交线，给出了判断两个平面是否相交的依据。作业课本第40页练习A1、2练习B1