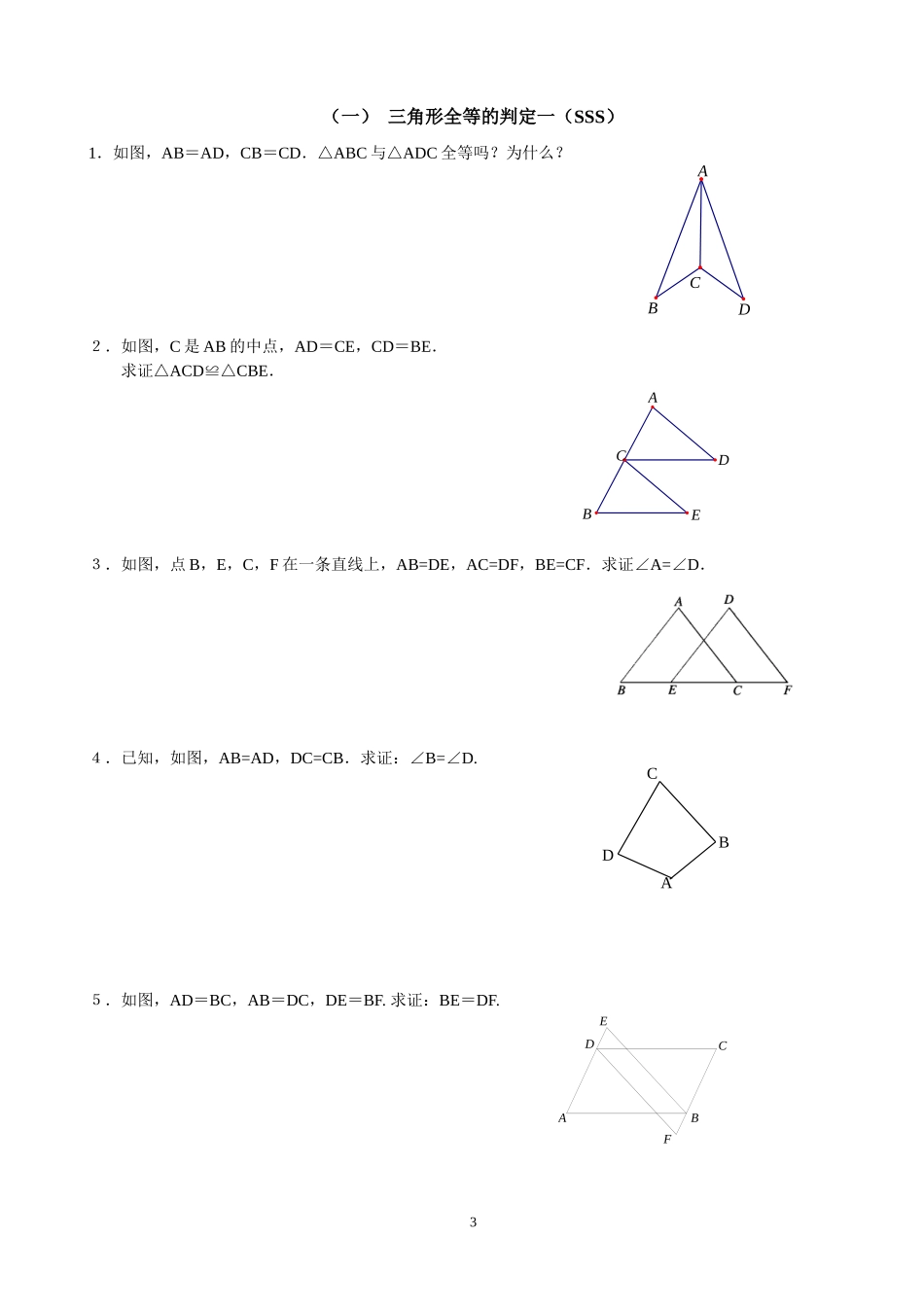
全等三角形一、全等三角形1、定义:能够完全重合的两个三角形叫做全等三角形。特征:形状相同、大小相等、完全重合。一个三角形经过平移、翻折、旋转可以得到它的全等形。平移、翻折、旋转前后的图形全等。2、全等三角形的表示:“全等”用“≌”表示,“∽”表示两图形的形状相同,“=”表示大小相等,读作“全等于”。注意:记两三角形全等时,通常把表示对应顶点的字母写在对应位置上。全等三角形的对应元素:对应顶点,对应边,对应角3、全等三角形的性质(1)全等三角形的对应边相等、对应角相等。(2)全等三角形的周长相等、面积相等。(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。4、全等三角形的判定(1)边边边:三边对应相等的两个三角形全等(可简写成“SSS”)(2)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)(3)角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)(4)角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)(5)斜边、直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)5、证明两个三角形全等的基本思路:二、角的平分线1、(性质)角的平分线上的点到角的两边的距离相等。2、(判定)角的内部到角的两边的距离相等的点在角的平分线上。1三、学习全等三角形应注意的问题(1)要正确区分“对应边”与“对边”,“对应角”与“对角”的不同含义;(2)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4)时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”。2FEDCBA(一)三角形全等的判定一(SSS)1.如图,AB=AD,CB=CD.△ABC与△ADC全等吗?为什么?2.如图,C是AB的中点,AD=CE,CD=BE.求证△ACD≌△CBE.3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证∠A=∠D.4.已知,如图,AB=AD,DC=CB.求证:∠B=∠D.5.如图,AD=BC,AB=DC,DE=BF.求证:BE=DF.3CDABDACBEADCB(二)三角形全等的判定二(SAS)1.如图,AC和BD相交于点O,OA=OC,OB=OD.求证DC∥AB.2.如图,△ABC≌△,AD,分别是△ABC,△的对应边上的中线,AD与有什么关系?证明你的结论.3.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.4.已知:如图,AD∥BC,AD=CB,求证:△ADC≌△CBA.5.已知:如图AD∥BC,AD=CB,AE=CF。求证:△AFD≌△CEB.6.已知,如图,AB=AC,AD=AE,∠1=∠2。求证:△ABD≌△ACE.4ACEDBAEBCFDABCD2ACBHED1HFEDCBA7.已知:如图,点B、E、C、F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.8.已知:如图,AD是BC上的中线,且DF=DE.求证:BE∥CF.9.如图,在△ABC中,分别延长中线BE、CD至F、H,使EF=BE,DH=CD,连结AF、AH.求证:(1)AF=AH;(2)点A、F、H三点在同一直线上;(3)HF∥BC.10.如图,在△ABC中,AC⊥BC,AC=BC,直线EF交AC于F,交AB于E,交BC的延长线于D,连结AD、BF,CF=CD.求证:BF=AD,BF⊥AD.11.证明:如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(提示:首先分清已知和求证,然后画出图形,再结合图形用数学符号表示已知和求证)5ABCDEF12.证明:如果两个三角形有两条边和第三边上的中线对应相等,那么这两个三角形全等.13.已知:如图,正方形ABCD,BE=CF,求证:(1)AE=BF;(2)AE⊥BF.14.已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证BE=AE+CF.(提示:旋转构造等腰)15.如图,△ABD和△ACE是△ABC外两个等腰直角三角形,∠BAD=∠CAE=900.(1)判断CD与BE有怎样的数量关系;(2)探索DC与BE的夹角的大小;(3)取BC的中点M,连MA,探讨MA与DE的位置关系.6ABCDEFGFEDCABABCDEF(三)(四)三角形全等的判定三、四(ASA、AAS)1.如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证AB=DE,AC=DF.2.如图,∠ACB=90°,AC=...