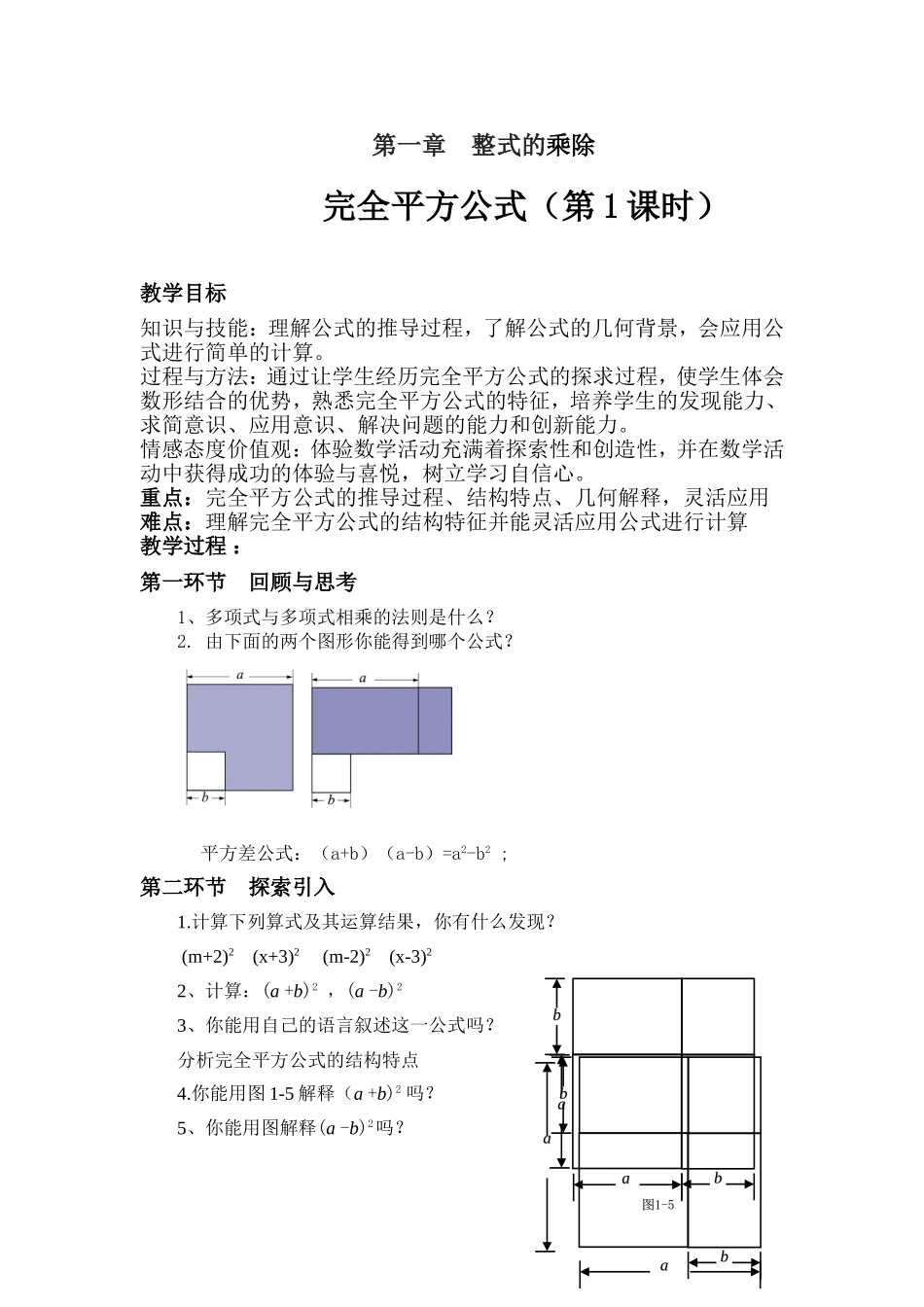
第一章整式的乘除完全平方公式(第1课时)教学目标知识与技能:理解公式的推导过程,了解公式的几何背景,会应用公式进行简单的计算。过程与方法:通过让学生经历完全平方公式的探求过程,使学生体会数形结合的优势,熟悉完全平方公式的特征,培养学生的发现能力、求简意识、应用意识、解决问题的能力和创新能力。情感态度价值观:体验数学活动充满着探索性和创造性,并在数学活动中获得成功的体验与喜悦,树立学习自信心。重点:完全平方公式的推导过程、结构特点、几何解释,灵活应用难点:理解完全平方公式的结构特征并能灵活应用公式进行计算教学过程:第一环节回顾与思考1、多项式与多项式相乘的法则是什么?2.由下面的两个图形你能得到哪个公式?平方差公式:(a+b)(a-b)=a2-b2;第二环节探索引入1.计算下列算式及其运算结果,你有什么发现?(m+2)2(x+3)2(m-2)2(x-3)22、计算:(a+b)2,(a-b)23、你能用自己的语言叙述这一公式吗?分析完全平方公式的结构特点4.你能用图1-5解释(a+b)2吗?5、你能用图解释(a-b)2吗?bbbbaaaa图图11-5-5bbbbaaaa第三环节典型剖析,正误辨析例1用完全平方公式计算:(1)(2x−3)2;(2)(4x+5y)2;(3)(mn−a)22.课堂检测.(1)计算:;;(n+1)2-n2(2)纠错练习:指出下列各式中的错误,并加以改正:(1)(2a+1)2=4a2+1(2)(2a−1)2=2a2−2a+1;(3)(-a−1)2=-a2−2a−1.第四环节课堂小结1.完全平方公式(a±b)2=a2±2ab+b2,首平方,尾平方,2倍乘积放中央,加减看前方。2.解题过程中要准确确定a和b,对照公式原形的两边,做到不丢项、不弄错符号、2ab时不少乘2.第五环节布置作业1.基础训练:教材习题P26.1,2,42.拓展练习:(a+b)2与(a-b)2有怎样的联系?能否用一个等式来表示两者之间的关系,并尝试用图形来验证你的结论?图图11--55