中考数学综合题专题【动点综合型问题二】专题解析VIP免费

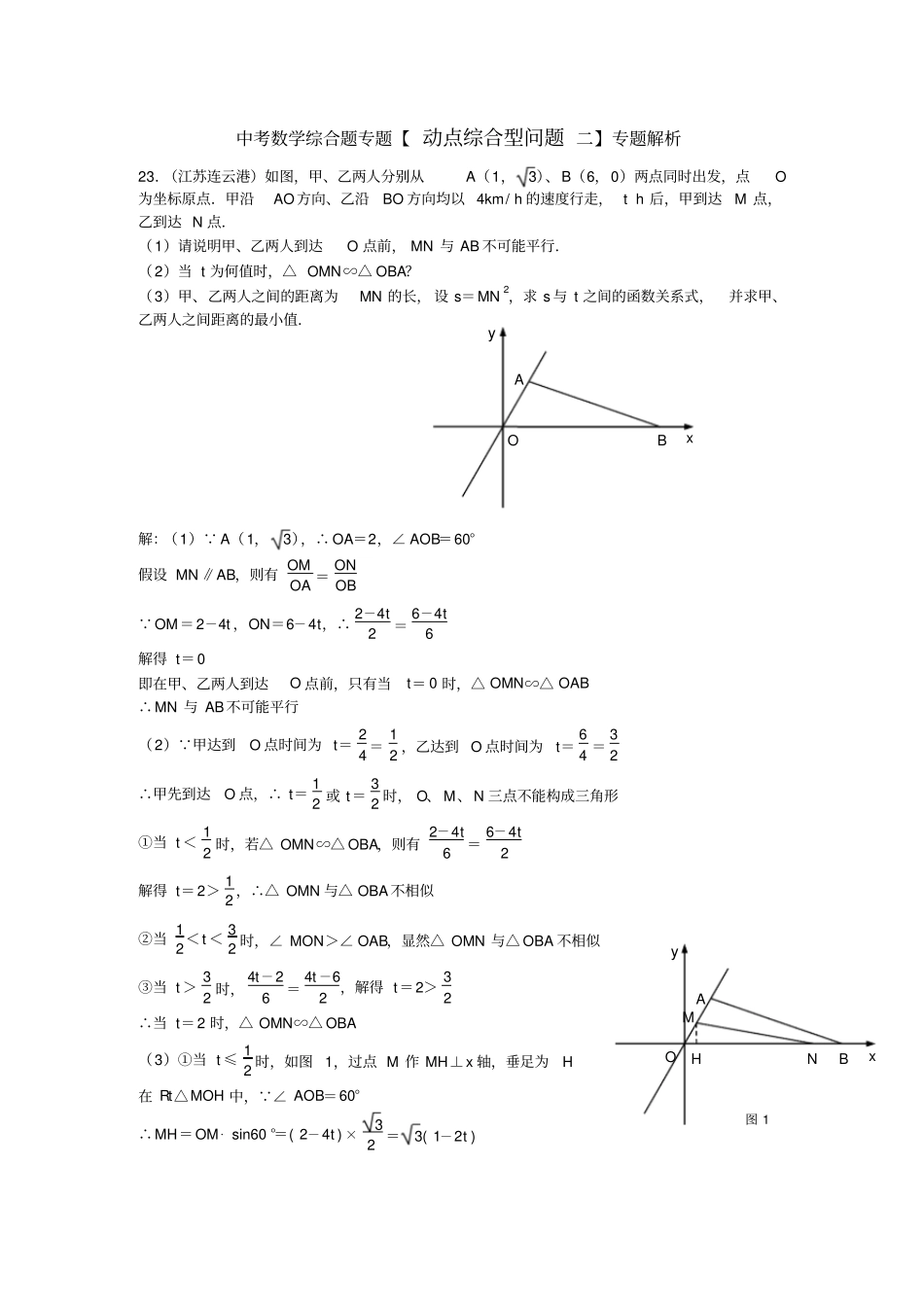
中考数学综合题专题【动点综合型问题二】专题解析23．（江苏连云港）如图，甲、乙两人分别从A（1，3）、B（6，0）两点同时出发，点O为坐标原点．甲沿AO方向、乙沿BO方向均以4km/h的速度行走，th后，甲到达M点，乙到达N点．（1）请说明甲、乙两人到达O点前，MN与AB不可能平行．（2）当t为何值时，△OMN∽△OBA？（3）甲、乙两人之间的距离为MN的长，设s＝MN2，求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值．解：（1） A（1，3），∴OA＝2，∠AOB＝60°假设MN∥AB，则有OMOA＝ONOB OM＝2－4t，ON＝6－4t，∴2－4t2＝6－4t6解得t＝0即在甲、乙两人到达O点前，只有当t＝0时，△OMN∽△OAB∴MN与AB不可能平行（2） 甲达到O点时间为t＝24＝12，乙达到O点时间为t＝64＝32∴甲先到达O点，∴t＝12或t＝32时，O、M、N三点不能构成三角形①当t＜12时，若△OMN∽△OBA，则有2－4t6＝6－4t2解得t＝2＞12，∴△OMN与△OBA不相似②当12＜t＜32时，∠MON＞∠OAB，显然△OMN与△OBA不相似③当t＞32时，4t－26＝4t－62，解得t＝2＞32∴当t＝2时，△OMN∽△OBA（3）①当t≤12时，如图1，过点M作MH⊥x轴，垂足为H在Rt△MOH中， ∠AOB＝60°∴MH＝OM·sin60°＝(2－4t)×32＝3(1－2t)OByxAOByxAMH图1N∴NH＝12(4t－2)＋(6－4t)＝5－2t∴s＝[3(1－2t)]2＋(5－2t)2＝16t2－32t＋28②当12＜t≤32时，如图2，作MH⊥x轴，垂足为H在Rt△MNH中，MH＝32(4t－2)＝3(2t－1)NH＝12(4t－2)＋(6－4t)＝5－2t∴s＝[3(1－2t)]2＋(5－2t)2＝16t2－32t＋28③当t＞32时，同理可得s＝[3(1－2t)]2＋(5－2t)2＝16t2－32t＋28综上所述，s＝16t2－32t＋28 s＝16t2－32t＋28＝16(t－1)2＋12∴当t＝1时，s有最小值为12∴甲、乙两人距离的最小值为23km24．（江苏南通）如图，在△ABC中，AB＝AC＝10厘米，BC＝12厘米，D是BC的中点．点P从B出发，以a厘米/秒（a＞0）的速度沿BA匀速向点A运动，点Q同时以1厘米/秒的速度从D出发，沿DB匀速向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为t秒．（1）若a＝2，△BPQ∽△BDA，求t的值；（2）设点M在AC上，四边形PQCM为平行四边形．①若a＝52，求PQ的长；②是否存在实数a，使得点P在∠ACB的平分线上？若存在，请求出a的值；若不存在，请说明理由．解：（1） BC＝12，D是BC的中点∴BD＝CD＝6 a＝2，∴BP＝2t，DQ＝t，BQ＝6－t △BPQ∽△BDA，∴BPBD＝BQBA∴2t6＝6－t10，∴t＝1813CBDAQPOByxAMH图2N（2）① a＝52，∴BP＝52t 四边形PQCM为平行四边形，∴PQ∥AC∴△BPQ∽△BAC，∴BPBA＝BQBC∴52t10＝6－t12，∴t＝32，∴BP＝154 AB＝AC，∴PQ＝BP＝154②不存在理由：假设存在实数a，使得点P在∠ACB的角平分线上则四边形PQCM为菱形，∴BP＝PQ＝CQ＝6＋t由①知，BPBA＝BQBC，∴6＋t10＝6－t12∴t＝－611＜0∴不存在实数a，使得点P在ACB的角平分线上25．（江苏宿迁）如图，在平面直角坐标系xOy中，已知直线l1：y＝12x与直线l2：y＝－x＋6相交于点M，直线l2与x轴相交于点N．（1）求M、N的坐标；（2）在矩形ABCD中，已知AB＝1，BC＝2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动．设矩形ABCD与△OMN的重合部分的面积为S，移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）．直接写出S与自变量t之间的函数关系式（不需要给出解答过程）；（3）在（2）的条件下，当t为何值时，S的值最大？并求出最大值．解：（1）对于y＝－x＋6，令y＝0，得x＝6∴点N的坐标为（6，0）由题意，得y＝12xy＝－x＋6解得x＝4y＝2ABl1NMxl2CDyOCBDAQPMABl1NMxl2CDyOAl1NMxl2CDyOB∴点M的坐标为（4，2）（2）当0≤t≤1时，S＝14t2当1＜t≤4时，S＝12t－14当4＜t＜5时，S＝－34t2＋132t－494当5≤t＜6时，S＝－t＋132当6≤t≤7时，S＝12(7－t)2（3）解法一：当0≤t≤1时，S最大＝14当1＜t≤4时，S最大＝74当4＜t＜5时，S＝－34(t－133)2＋116∴当t＝133时，S最大＝116当5≤t＜6时，S最大＝32当6≤t≤7时，S最大＝12综上可知，当t＝133时，S的值最大，且最大值是116解法二：由（2）中的函数关系式可知，S的最大值一定在4＜t...