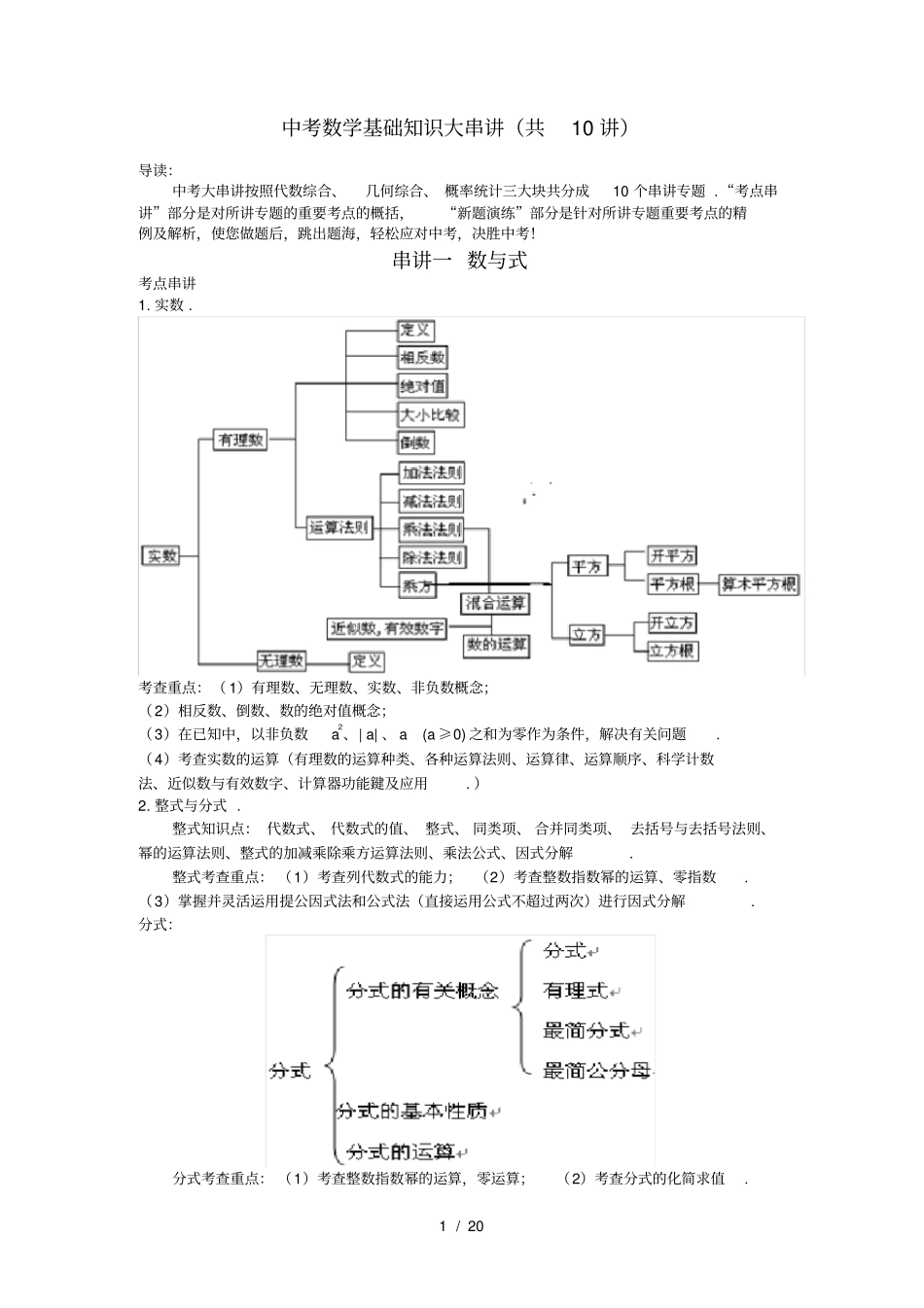
1/20中考数学基础知识大串讲(共10讲)导读:中考大串讲按照代数综合、几何综合、概率统计三大块共分成10个串讲专题.“考点串讲”部分是对所讲专题的重要考点的概括,“新题演练”部分是针对所讲专题重要考点的精例及解析,使您做题后,跳出题海,轻松应对中考,决胜中考!串讲一数与式考点串讲1.实数.考查重点:(1)有理数、无理数、实数、非负数概念;(2)相反数、倒数、数的绝对值概念;(3)在已知中,以非负数a2、|a|、a(a≥0)之和为零作为条件,解决有关问题.(4)考查实数的运算(有理数的运算种类、各种运算法则、运算律、运算顺序、科学计数法、近似数与有效数字、计算器功能鍵及应用.)2.整式与分式.整式知识点:代数式、代数式的值、整式、同类项、合并同类项、去括号与去括号法则、幂的运算法则、整式的加减乘除乘方运算法则、乘法公式、因式分解.整式考查重点:(1)考查列代数式的能力;(2)考查整数指数幂的运算、零指数.(3)掌握并灵活运用提公因式法和公式法(直接运用公式不超过两次)进行因式分解.分式:分式考查重点:(1)考查整数指数幂的运算,零运算;(2)考查分式的化简求值.2/203.二次根式.式子a(a≥0)叫做二次根式.考查重点:(1)了解二次根式、最简二次根式、同类二次根式的概念,会辨别最简二次根式和同类二次根式.掌握二次根式的性质,会化简简单的二次根式,能根据指定字母的取值范围将二次根式化简;(2)掌握二次根式的运算法则,能进行二次根式的加减乘除四则运算,会进行简单的分母有理化.新题演练:新题1:在实数-23,0,3,-3.14,2,4,-0.1010010001⋯(每两个1之间依次多1个0),sin30°这8个实数中,无理数有()A.1个B.2个C.3个D.4个解析:对实数分类,不能只为表面形式迷惑,而应从最后结果去判断.首先明确无理数的概念,即“无限不循环小数叫做无理数”.一般来说,用根号表示的数不一定就是无理数,如4=2是有理数,关键在于这个形式上带根号的数的最终结果是不是无限不循环小数.同样,用三角符号表示的数也不一定就是无理数,如sin30°、tan45°等.而-0.1010010001⋯尽管有规律,?但它是无限不循环小数,是无理数.2是无理数,而不是分数.在上面所给的实数中,只有3,2,-0.1010010001⋯这三个数是无理数,其他五个数都是有理数,故选C.答案:C新题2:已知x、y是实数,且34x+(y2-6y+9)=0,若axy-3x=y,则实数a的值是()A.14B.-14C.74D.-74解析:若几个非负数之和等于零,则每个非负数均等于零.这是非负数具有的一个重要性质.本题中 34x和(y-3)2均为非负数,它们的和为零,只有3x+4=0,且y-3=0,由此可求得x,y的值,将其代入axy-3x=y中,即求得a的值.答案:34x+(y-3)2=0∴3x+4=0,y-3=0∴x=-43,y=3. axy-3x=y,∴-43×3a-3×(-43)=3∴a=14∴选A新题3:若a,b,c是三角形三边的长,则代数式a2+b2-c2-2ab的值()A.大于零B.小于零C.大于或等于零D.小于或等于零3/20解析:本题是确定代数式的取值范围与因式分解的综合题,?把所给多项式的部分因式进行因式分解,再结合“a,b,c是三角形的三边”,应满足三角形三边关系是解决这类问题的常用方法.答案:(1) a2+b2-c2-2ab=(a2-2ab+b2)-c2=(a-b)2-c2=(a-b+c)(a-b-c),又 a,b,?c是三角形三边的长.∴a+c>b,a0,a-b-c<0∴(a-b+c)(a-b-c)<0即a2+b2-c2-2ab<0,故选B.新题4:先化简22424422xxxxxxx,然后请你任取一个合适的数作为x的值代入求值.解析:本题考查整式的因式分解及分式的加减乘除混和运算,要注意运算顺序.先乘除后加减,有括号先算括号里的或按照乘法的分配律去括号.22424422xxxxxxx22222222xxxxxxxxx2222xxxxx2222822xxxxx.取值时要考虑分式的意义,即x≠±2.答案:原式=22424422xxxxxxx22222222xxxxxxxxx2222xxxxx2222822xxxxx(x只要不取±2均可)取x=6,得原式=1串讲二方程(组)与不等式(组)考点串讲1.一元一次方程.知识点:等式及基本性质、方程、方程的解、解方程、一元一次方程.考查重点:掌握解一元一次方程的一般步骤,能熟练地解一元一次方程.2.二...