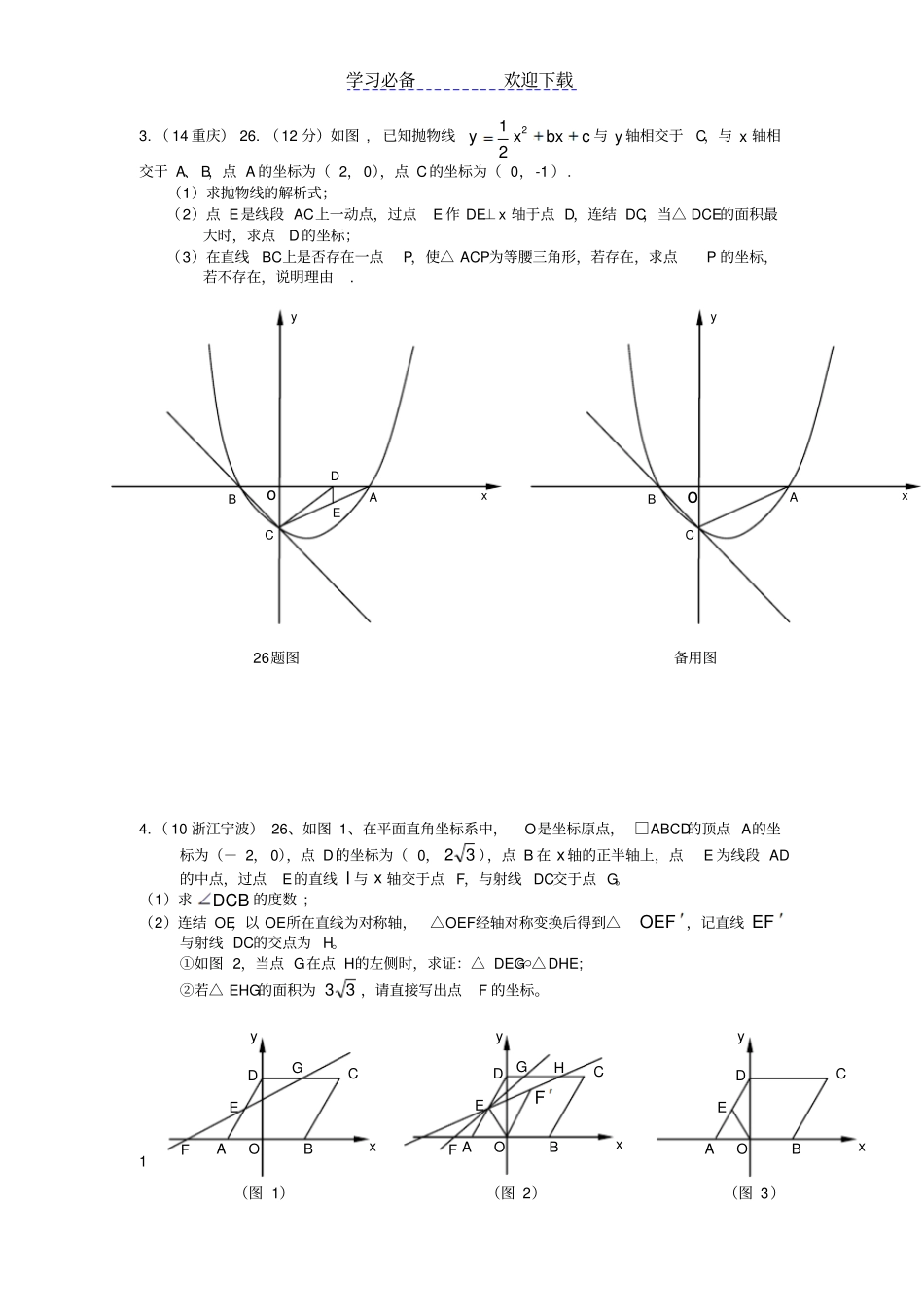
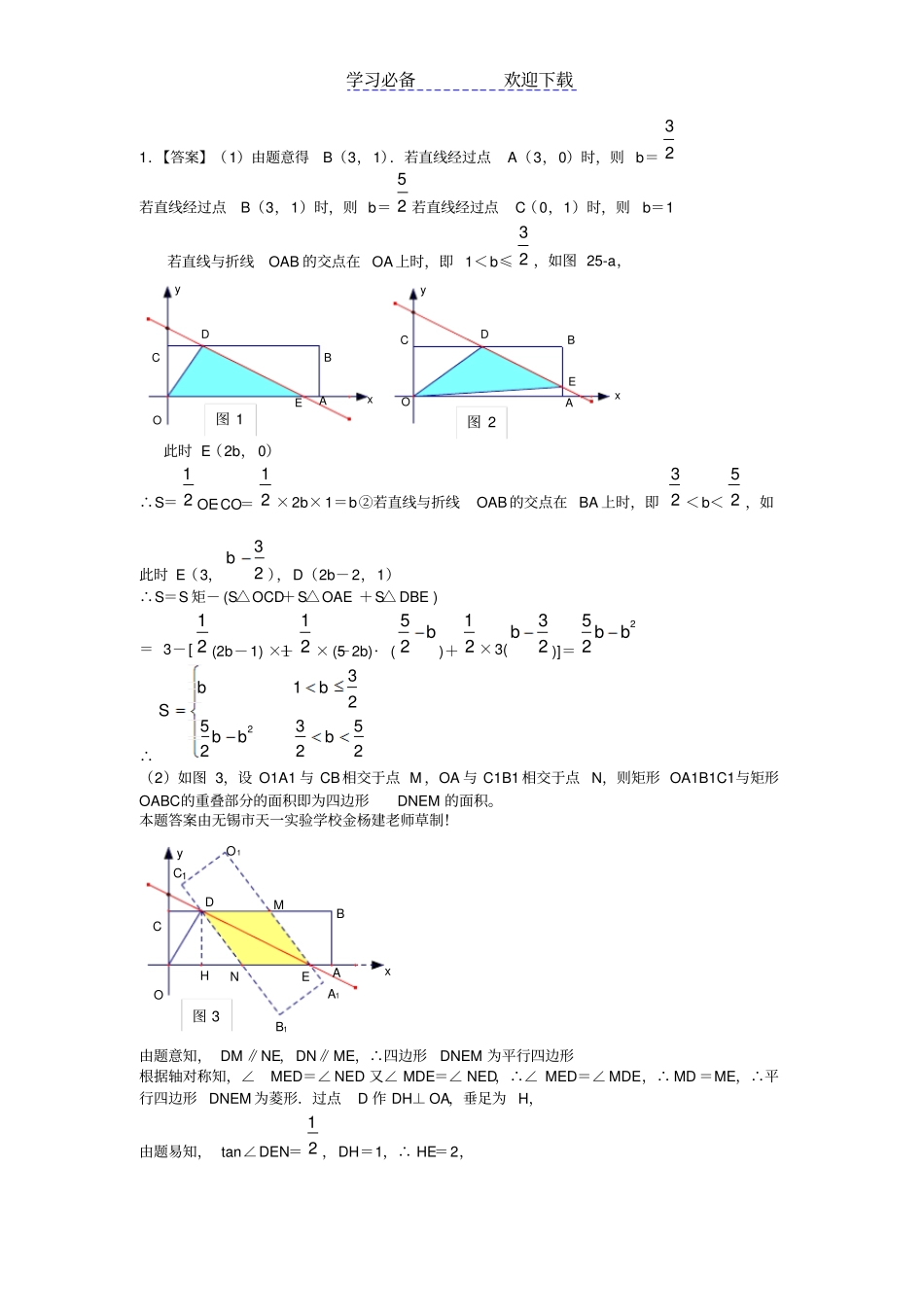
学习必备欢迎下载中考数学精选1,(2014广东,25,14分)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-12x+b交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.2(浙江台州).如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.(1)求证:△DHQ∽△ABC;(2)求y关于x的函数解析式并求y的最大值;(3)当x为何值时,△HDE为等腰三角形?CDBAEOxy(第24题)DEQBACPH学习必备欢迎下载3.(14重庆)26.(12分)如图,已知抛物线cbxxy221与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).(1)求抛物线的解析式;(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由.4.(10浙江宁波)26、如图1、在平面直角坐标系中,O是坐标原点,□ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,32),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G。(1)求DCB的度数;(2)连结OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△FOE,记直线FE与射线DC的交点为H。①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;②若△EHG的面积为33,请直接写出点F的坐标。1ABCEDxyo题图26ABCxyo备用图yxCDAOBEGF(图1)xCDAOBEGHFFy(图2)xCDAOBEy(图3)学习必备欢迎下载1.【答案】(1)由题意得B(3,1).若直线经过点A(3,0)时,则b=32若直线经过点B(3,1)时,则b=52若直线经过点C(0,1)时,则b=1若直线与折线OAB的交点在OA上时,即1<b≤32,如图25-a,此时E(2b,0)∴S=12OE·CO=12×2b×1=b②若直线与折线OAB的交点在BA上时,即32<b<52,如此时E(3,32b),D(2b-2,1)∴S=S矩-(S△OCD+S△OAE+S△DBE)=3-[12(2b-1)×1+12×(5-2b)·(52b)+12×3(32b)]=252bb∴2312535222bbSbbb(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。本题答案由无锡市天一实验学校金杨建老师草制!由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形根据轴对称知,∠MED=∠NED又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.过点D作DH⊥OA,垂足为H,由题易知,tan∠DEN=12,DH=1,∴HE=2,DExyCBAO图2图3HNMC1A1B1O1DExyCBAO图1DExyCBAO学习必备欢迎下载设菱形DNEM的边长为a,则在Rt△DHM中,由勾股定理知:222(2)1aa,∴54a∴S四边形DNEM=NE·DH=54∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为54.2台州.(14分)(1) A、D关于点Q成中心对称,HQ⊥AB,∴CHQD=90°,HD=HA,∴AHDQ,⋯⋯⋯⋯⋯⋯∴△DHQ∽△ABC.⋯⋯⋯⋯分(2)①如图1,当5.20x时,ED=x410,QH=xAAQ43tan,此时xxxxy4152343)410(212.当45x时,最大值3275y.②如图2,当55.2x时,ED=104x,QH=xAAQ43tan,此时xxxxy4152343)104(212.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分当5x时,最大值475y.∴y与x之间的函数解析式为).55.2(41523),5.20(4152322xxxxxxyy的最大值是475.(3)①如图1,当5.20x时,若DE=DH, DH=AH=xAQA45cos,DE=x410,∴x410=x45,2140x.显然ED=EH,HD=HE不可能;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分②如图2,当55.2x时,若DE=DH,104x=x45,1140x;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分若HD=HE,此时点D,E分别与点B,A重合,5x;DHQEBACP(图1)HQDEPBAC...