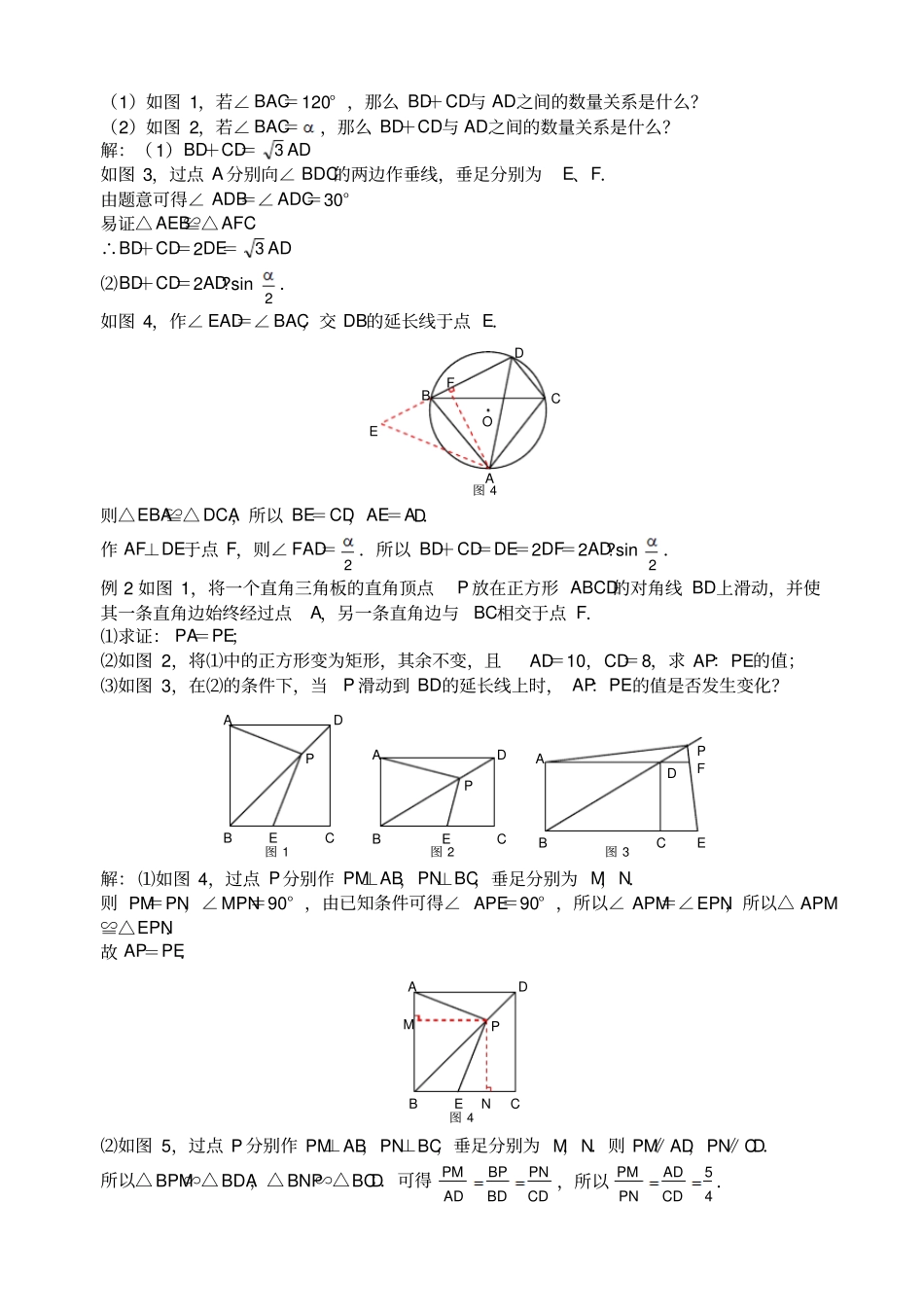
专题16《对角互补模型》破解策略1.全等型之“90°”如图,∠AOB=∠DCE=90°,OC平分∠AOB,则(1)CD=CE;(2)OD+OE=2OC;(3)212OCDOCESSOC.证明方法一:如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N.由角平分线的性质可得CM=CN,∠MCN=90°.所以∠MCD=∠NCE,从而△MCD≌△NCE(ASA),故CD=CE.易证四边形MONC为正方形.所以OD+OE=OD+ON+NE=2ON=2OC.所以2212OCDOCEMONCSSSONOC正方形.方法二:如图,过C作CF⊥OC,交OB于点F.易证∠DOC=∠EFC=45°,CO=CF,∠DCO=∠ECF.所以△DCO≌△ECF(ASA)所以CD=CE,OD=FE,可得OD+OE=OF=2OC.所以212OCDOCEOCFSSSOC.【拓展】如图,当∠DCE的一边与AO的延长线交于点D时,则:(1)CD=CE;(2)OE-OD=2OC;(3)212OCEOCDSSOC.如图,证明同上.2.全等型之“120”如图,∠AOB=2∠DCE=120°,OC平分∠AOB,则:(1)CD=CE;(2)OD+OE=OC;(3)234OCDOCESSOC.证明方法一:如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N.NMAOBDCEFAOBDCE所以2324OCDOCEONCSSSOC易证△MCD≌△NCE(ASA),所以CD=CE,OD+OE=2ON=OC.方法二:如图,以CO为一边作∠FCO=60°,交OB于点F,则△OCF为等边三角形.易证△DCO≌△ECF(ASA).所以CD=CE,OD+OE=OF=OC,∴S△OCD+S△OCE=S△OCF=43OC2【拓展】如图,当∠DCE的一边与BO的延长线交于点E时,则:(1)CD=CE;(2)OD-OE=OC;(3)S△OCD-S△OCE=43OC2如图,证明同上.3、全等型之“任意角”如图,∠AOB=2,∠DCE=180°-2,OC平分∠AOB,则:(1)CD=CE;(2)OD+OE=2OC·cos;(3)S△ODC+S△OEC=OC2·sincos证明:方法一:如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M,N易证△MCD≌△NCE(ASA)∴CD=CE,OD+OE=2ON=2OC·cos∴S△ODC+S△OEC=2S△ONC=OC2·sincos方法二:如图,以CO为一边作∠FCO=180°-2,交OB于点F.易证△DCO≌△ECF(ASA)∴CD=CE,OD+OE=OF=2OC·cos∴S△ODC+S△OEC=S△OCF=OC2·sincos【拓展】如图,当∠DCE的一边与BO的延长线交于点E时,则:(1)CD=CE;(2)OD-OE=2OC·cos;(3)S△ODC-S△OEC=OC2·sincos如图,证明同上4、相似性之“90°”如图,∠AOB=∠DCE=90°,∠COB=,则CE=CD·tan方法一:如图,过点C分别作CM⊥OA,CN⊥OB,垂足分别为M、N易证△MCD∽△NCE,∴tanCMCNCDCEMDNE,即CE=CD·tan方法二:如图,过点C作CF⊥OC,交OB于点F.易证△DCO∽△ECF,∴tanCOCFCDCEODFE,即CE=CD·tan方法三:如图,连接DE.易证D、O、E、C四点共圆∴∠CDE=∠COE=,故CE=CD·tan【拓展】如图,当∠DCE的一边与AO的延长线交于点D时,则CE=CD·tan如图,证明同上.例题讲解例1、已知△ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧BC上任取一点D,连接AD,BD,CD.MNEOBACD(1)如图1,若∠BAC=120°,那么BD+CD与AD之间的数量关系是什么?(2)如图2,若∠BAC=,那么BD+CD与AD之间的数量关系是什么?解:(1)BD+CD=3AD如图3,过点A分别向∠BDC的两边作垂线,垂足分别为E、F.由题意可得∠ADB=∠ADC=30°易证△AEB≌△AFC∴BD+CD=2DE=3AD⑵BD+CD=2AD?sin2.如图4,作∠EAD=∠BAC,交DB的延长线于点E.则△EBA≌△DCA,所以BE=CD,AE=AD.作AF⊥DE于点F,则∠FAD=2.所以BD+CD=DE=2DF=2AD?sin2.例2如图1,将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动,并使其一条直角边始终经过点A,另一条直角边与BC相交于点F.⑴求证:PA=PE;⑵如图2,将⑴中的正方形变为矩形,其余不变,且AD=10,CD=8,求AP:PE的值;⑶如图3,在⑵的条件下,当P滑动到BD的延长线上时,AP:PE的值是否发生变化?解:⑴如图4,过点P分别作PM⊥AB,PN⊥BC,垂足分别为M,N.则PM=PN,∠MPN=90°,由已知条件可得∠APE=90°,所以∠APM=∠EPN,所以△APM≌△EPN.故AP=PE.⑵如图5,过点P分别作PM⊥AB,PN⊥BC,垂足分别为M,N.则PM∥AD,PN∥CD.所以△BPM∽△BDA,△BNP∽△BCD.可得PMBPPNADBDCD,所以54PMADPNCD.图4ADPBECNM图3ADBEPFCADBPCE...