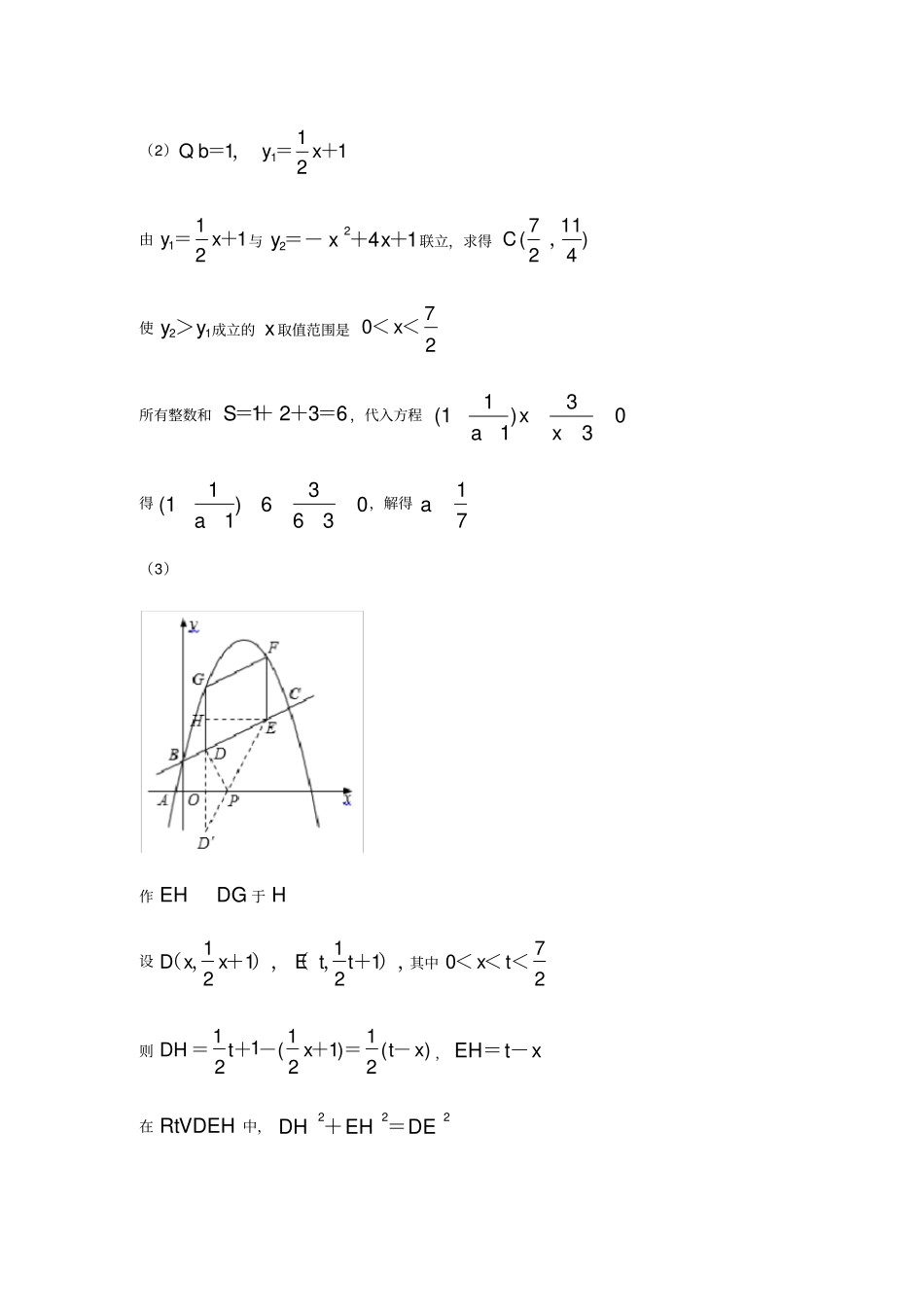
4.因动点产生的将军饮马问题1.如图,一次函数112yxb=+的图象l与二次函数22yxmxb=-++的图象C都经过点01B(,)和点C,且图象C过点250A(,).(1)求二次函数的最大值;(2)设使21yy>成立的x取值的所有整数和为S,若S是关于x的方程13(1)013xax的根,求a的值;(3)若点FG、在图象C上,长度为5的线段DE在线段BC上移动,EF与DG都始终平行于y轴.当四边形DEFG的面积最大时,在x轴上求一点P,使PDPE+最小,求出点P的坐标.解析:(1)把25001AB(,)、(,)代入22yxmxb=-++解得41mb=,=∴二次函数的解析式为2241yxx=-++22241(25)yxxxQ=-++=--+∴二次函数的最大值为5(2)11112byxQ=,=+由1211yx=+与2241yxx=-++联立,求得711()24C,使21yy>成立的x取值范围是702x<<所有整数和1236S=++=,代入方程13(1)013xax得13(1)60163a,解得17a(3)作EHDG于H设111212DxxEtt(,+),(,+),其中702xt<<<则1111()()2221DHtxtx=+-+=-,EHtx=-在RtDEHV中,222DHEHDE+=即2221()()(5)4txtx-+-=22txtx-=,=+21412()212GxxxExx(,-++),(+,++),2()2221(4)Fxxx(+,-++++)由题意,四边形DEFG为梯形,要使面积最大,则DGEF+最大而2211()41124212()()[1()]22DGEFxxxxxx+=-++-+-++++-++223323323(8)4xxx=-++=--+∴当34x=时,四边形DEFG的面积最大3111119(),()4848DE,,作点D关于x轴的对称点D,连接DE交x轴于点P,则点P为所求311()48D,,易求直线DE的解析式为1589832yx令0y=,解得8960x89(0)60P,2.已知:直线2ly:=-,抛物线2yaxbxc=++的对称轴是y轴,且经过点0120(,-),(,).(1)求抛物线的解析式;(2)如图①,点P是抛物线上任意一点,过点P作直线l的垂线,垂足为Q.求证:POPQ=.(3)请你参考(2)中结论解决下列问题:①如图②,过原点作任意直线AB,交抛物线于点AB、.分别过AB、两点作直线l的垂线,垂足分别为MN、,连接OMON、,求证:OMON;②如图③,点11D(,),试探究在抛物线上是否存在点F,使得FDFO+取得最小值.若存在,求出点F的坐标;若不存在,请说明理由.解析:(1) 抛物线2yaxbxc=++的对称轴是y轴2yaxc=+,把0120(,-),(,)代入,得:140cac解得141ac∴抛物线的解析式为2114yx=-(2)设21(1)4Pmm,,则2141OEmPEm=,=-221211144PQmm=-+=+222114POOEPEmPOPQ=(3)AMlBNlAMBNOCQPP①,,AMOMOCBNONOC=,=由(2)知,AMAOBNBO=,=AOMAMOBONBNO=,=AOMMOCBONNOC=,=180AOMMOCBONNOCQ+++=90MOCNOC+=OMON②作FHlH于,则FDFOFDFH+=+当DFH、、三点在同一条直线上时,FDFO+取得最小值把1x=代入2114yx,得34y∴满足条件的点F的坐标为314(,-)3.已知平面直角坐标系中两定点1040AB(-,)、(,),抛物线220yaxbxa=+-()过点AB、,顶点为C,点0Pmnn(,)(<)为抛物线上一点.(1)求抛物线的解析式和顶点C的坐标;(2)当APB为钝角时,求m的取值范围;(3)若32m>,当APB为直角时,将该抛物线向左或向右平移502tt(<<)个单位,点CP、平移后对应的点分别记为CP、,是否存在t,使得首尾依次连接ABPC、、、所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.解析:(1) 抛物线22yaxbx=+-过点1040AB(-,)、(,)2016420abab解得1232kb∴抛物线的解析式为221322yxx=--22132213252()228yxxxQ=--∴顶点C的坐标为325()28,(2)若P点在x轴上方,显然PAB或PBA为钝角,则APB必为锐角,不合题意若P点在x轴下方,当P点与抛物线和y轴交点02D(,-)时2225ADOAOD=+=,22222025BDOBODAB=+=,=22290ADBDABADB+=,=由抛物线的对称性可知,点D关于抛物线对称轴的对称点32E(,-)也满足90AEB=以AB为直径作圆,则DE、均在圆上,抛物线上点A到D及E到B之间的部分在圆内当P点在这两个范围内运动时,满足APB为钝角10m-<<或34m<<(3)32mQ>,APB为直角∴由(2)知P点坐标为32(,-)由平移的性质知PCPC=ABQ与PC均为定值,要使ABPC、、、所...