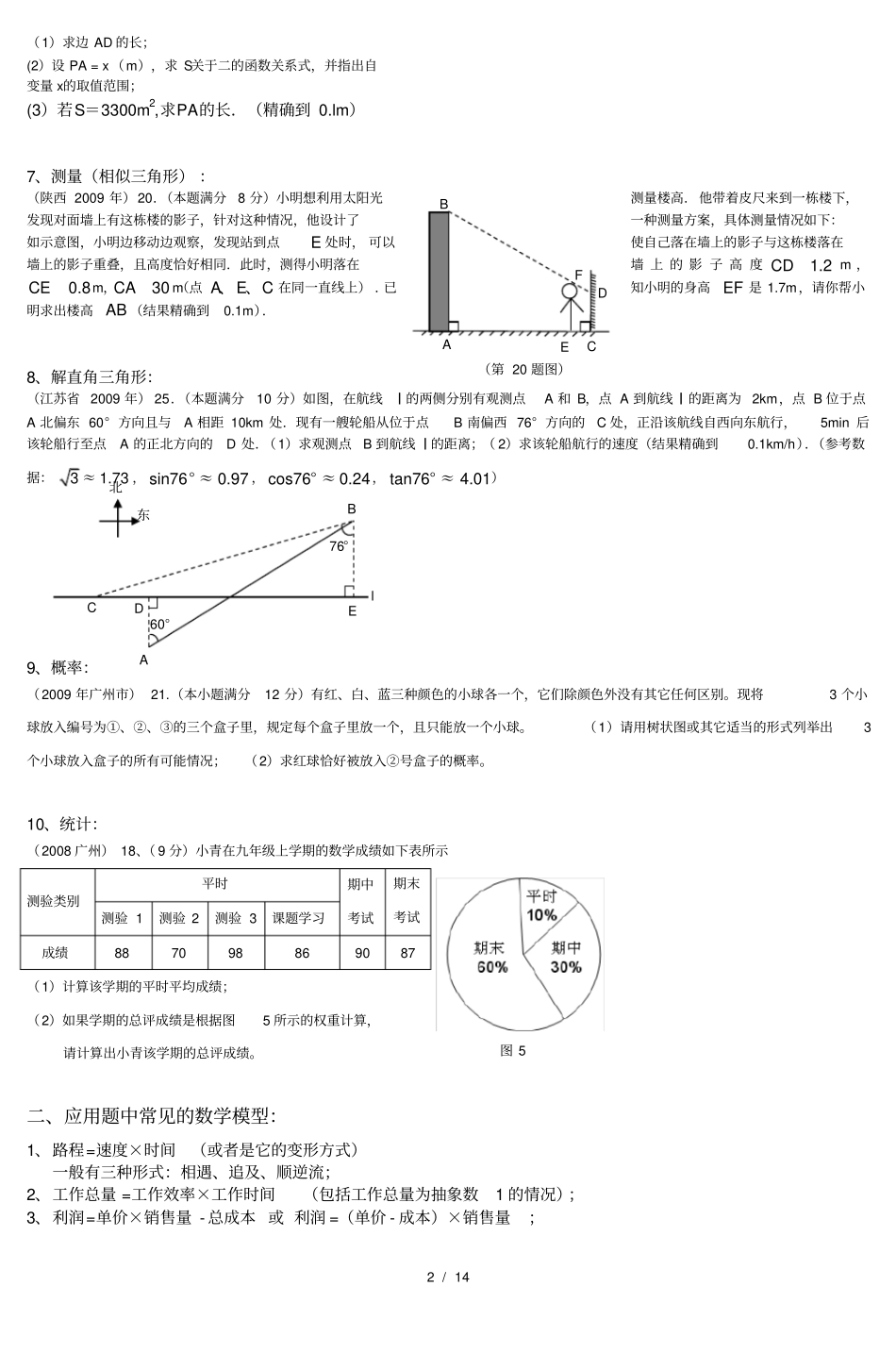
1/14中考应用题大题复习一、应用题的常见知识归属:1、分式方程:(2008广州)22、(12分)2008年初我国南方发生雪灾,某地电线被雪压断,供电局的维修队要到30千米远的郊区进行抢修。维修工骑摩托车先走,15分钟后,抢修车装载所需材料出发,结果两车同时到达抢修点。已知抢修车的速度是摩托车速度的1.5倍,求两种车的速度。2、方程组:(2009年广州市)23.、(本小题满分12分)为了拉动内需,广东启动“家电下乡”活动。某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出960台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1228台。(1)在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为多少台?(2)若Ⅰ型冰箱每台价格是2298元,Ⅱ型冰箱每台价格是1999元,根据“家电下乡”的有关政策,政府按每台冰箱价格的13%给购买冰箱的农户补贴,问:启动活动后的第一个月销售给农户的1228台Ⅰ型冰箱和Ⅱ型冰箱,政府共补贴了多少元(结果保留2个有效数字)?3、不等式(组)(2007年广州市)23、(12分)某博物馆的门票每张10元,一次购买30张到99张门票按8折优惠,一次购买100张以上(含100张)按7折优惠。甲班有56名学生,乙班有54名学生。(1)若两班学生一起前往参观博物馆,请问购买门票最少共需花费多少元?(2)当两班实际前往该博物馆参观的总人数多于30人且不足100人时,至少要多少人,才能使得按7折优惠购买100张门票比实际人数按8折优惠购买门票更便宜?4、一元二次方程:(2008年广东省)15.(本题满分6分)如图4,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长。5、一次函数:(2005广东省--非课改区)21、今年以来,广东大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:(1)分别写出当0≤x≤100和x≥100时,y与x的函数关系式;(2)利用函数关系式,说明电力公司采取的收费标准;(3)若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?6、二次函数:(广州市2005年)24.(本小题满分14分)如图1I,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB//DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为s的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.图42/14(1)求边AD的长;(2)设PA=x(m),求S关于二的函数关系式,并指出自变量x的取值范围;(3)若S=3300m2,求PA的长.(精确到0.lm)7、测量(相似三角形):(陕西2009年)20.(本题满分8分)小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子高度1.2CDm,墙上的影子重叠,且高度恰好相同.此时,测得小明落在知小明的身高EF是1.7m,请你帮小0.8CEm,30CAm(点AEC、、在同一直线上).已明求出楼高AB(结果精确到0.1m).8、解直角三角形:(江苏省2009年)25.(本题满分10分)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.(1)求观测点B到航线l的距离;(2)求该轮船航行的速度(结果精确到0.1km/h).(参考数据:31.73≈,sin760.97°≈,cos760.24°≈,tan764.01°≈)9、概率:(2009年广州市)21.(本小题满分12分)有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别。现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球。(1)请用树状图或其它适当的形式列举出3...