2014-2015高二第一学期数学周练（十六）理科VIP免费

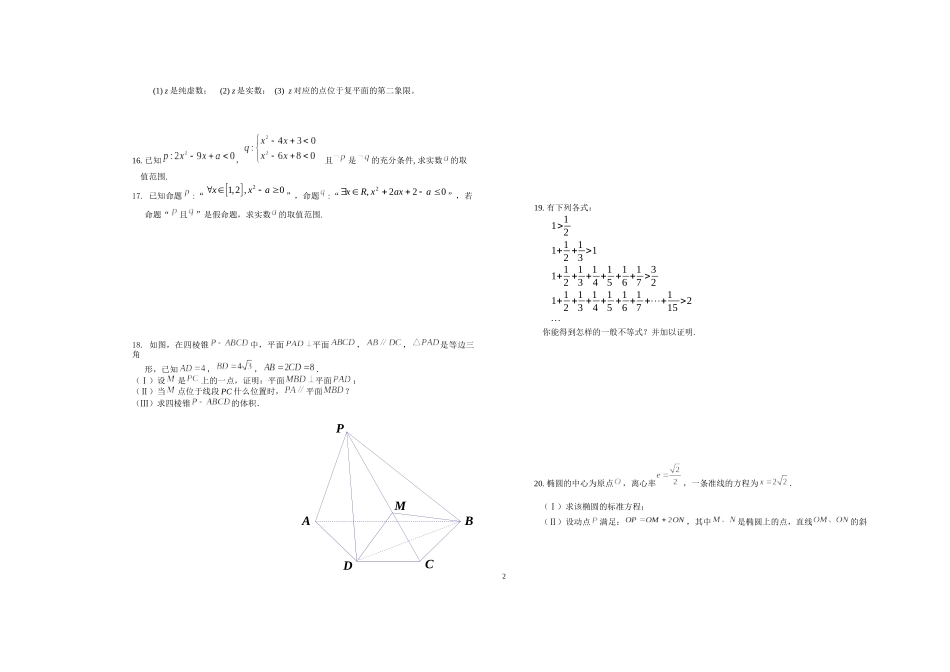
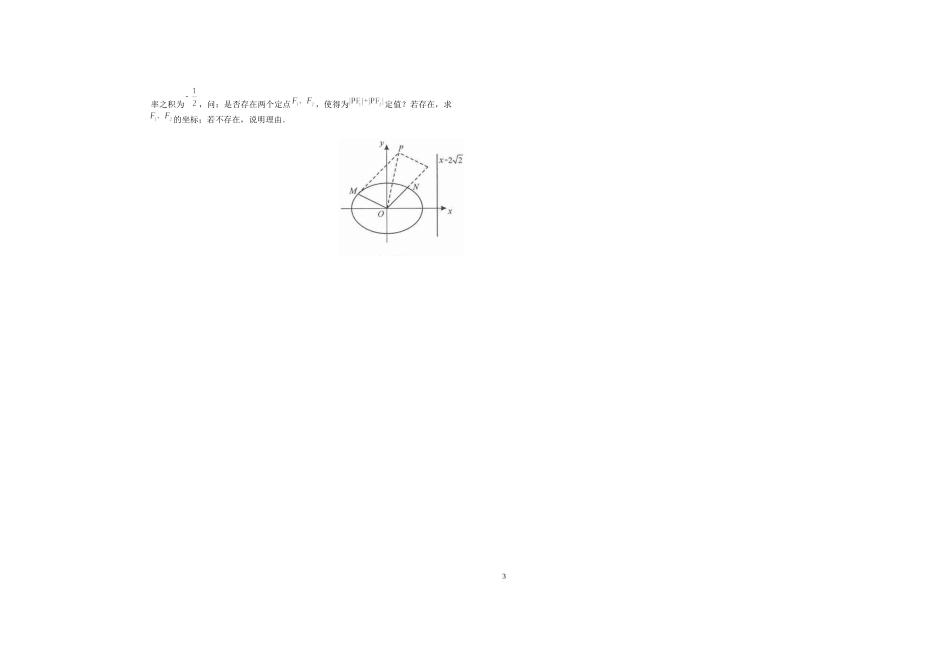
2014-2015高二第一学期数学周练（十六）理科一、填空题：本大题共14小题，每小题5分，共70分．把答案填写在答题纸相应位置.1.设x,y∈R，x1−i−y1−2i=51−3i，则x+y=2.若z∈C，|z+2−2i|=1,则|z−2−2i|的最小值是3.命题“若，则”与其逆命题、否命题、逆否命题四个命题中，真命题的个数是______4.若命题的逆命题是，命题的逆否命题是，则与的关系是.（在“互为逆命题”、“互为否命题”、“互为逆否命题”、“不能确定”中选择答案)5.已知：“：方程的解是”，“：方程的解是”，则“且”形式的命题为。6.命题“存在，使得”的否定是.7.命题“若，则”的否命题是___________.8.设.条件甲:三点构成以为直角顶点的三角形，条件乙：点的坐标是方程ax2+by2=c(ab≠0,c>0)的解，则甲是乙的条件.(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选择答案)9.给出下列四个命题：①若命题“”为真命题，则命题“”为真命题；②“菱形的两条对角线互相平分”的逆命题；③对于命题且，若假真，则且为假；④“有两条边相等且有一个角是”是一个三角形为等边三角形的充要条件.其中正确命题的序号为___.10.若数列na是等差数列，对于)(121nnaaanb，则数列nb也是等差数列。类比上述性质，若数列nc是各项都为正数的等比数列，对于0nd，则nd=时，数列nd也是等比数列。11.设为椭圆的焦点,过且垂直于轴的直线与椭圆交于A,B两点,若△为锐角三角形,则该椭圆离心率的取值范围是12.已知双曲线的两条渐近线的夹角为，则双曲线的离心率为。13.已知一个正三棱台的两个底面的边长分别等于8cm和18cm，侧棱长等于13cm，则它的侧面积为.14.以下四个关于圆锥曲线的命题中：①设A、B为两个定点，k为非零常数，若kPBPA，则动点P的轨迹为双曲线；②过定圆C上一定点A作圆的动弦AB、O为坐标原点，若OP21(OBOA)，则动点P的轨迹为椭圆；③方程2x2－5x＋2＝0的两根可分别作为椭圆和双曲线的离心率；④双曲线192522yx与13522yx有相同的焦点．其中真命题的序号为（写出所有真命题的序号）．二、解答题：本大题共6小题，共90分.请将解答填写在答题纸规定的区域内，否则答题无效.解答应写出文字说明、证明过程或演算步骤.15.设复数z=lg(m2−2m−2)+(m2+3m+2)i(m∈R)，试求实数m的取值，使得1(1)z是纯虚数；(2)z是实数；(3)z对应的点位于复平面的第二象限。16.已知，且是的充分条件,求实数的取值范围.17.已知命题:“21,2,0xxa”，命题:“022,2aaxxRx”，若命题“且”是假命题，求实数的取值范围.18.如图，在四棱锥中，平面平面，，是等边三角形，已知，，．（Ⅰ）设是上的一点，证明：平面平面；（Ⅱ）当点位于线段PC什么位置时，平面？（Ⅲ）求四棱锥的体积．19.有下列各式：1>121+12+13>11+12+13+14+15+16+17>321+12+13+14+15+16+17++115>2你能得到怎样的一般不等式？并加以证明.20.椭圆的中心为原点，离心率，一条准线的方程为．（Ⅰ）求该椭圆的标准方程；（Ⅱ）设动点满足：，其中是椭圆上的点，直线的斜MDCAPB2率之积为，问：是否存在两个定点，使得为定值？若存在，求的坐标；若不存在，说明理由．3