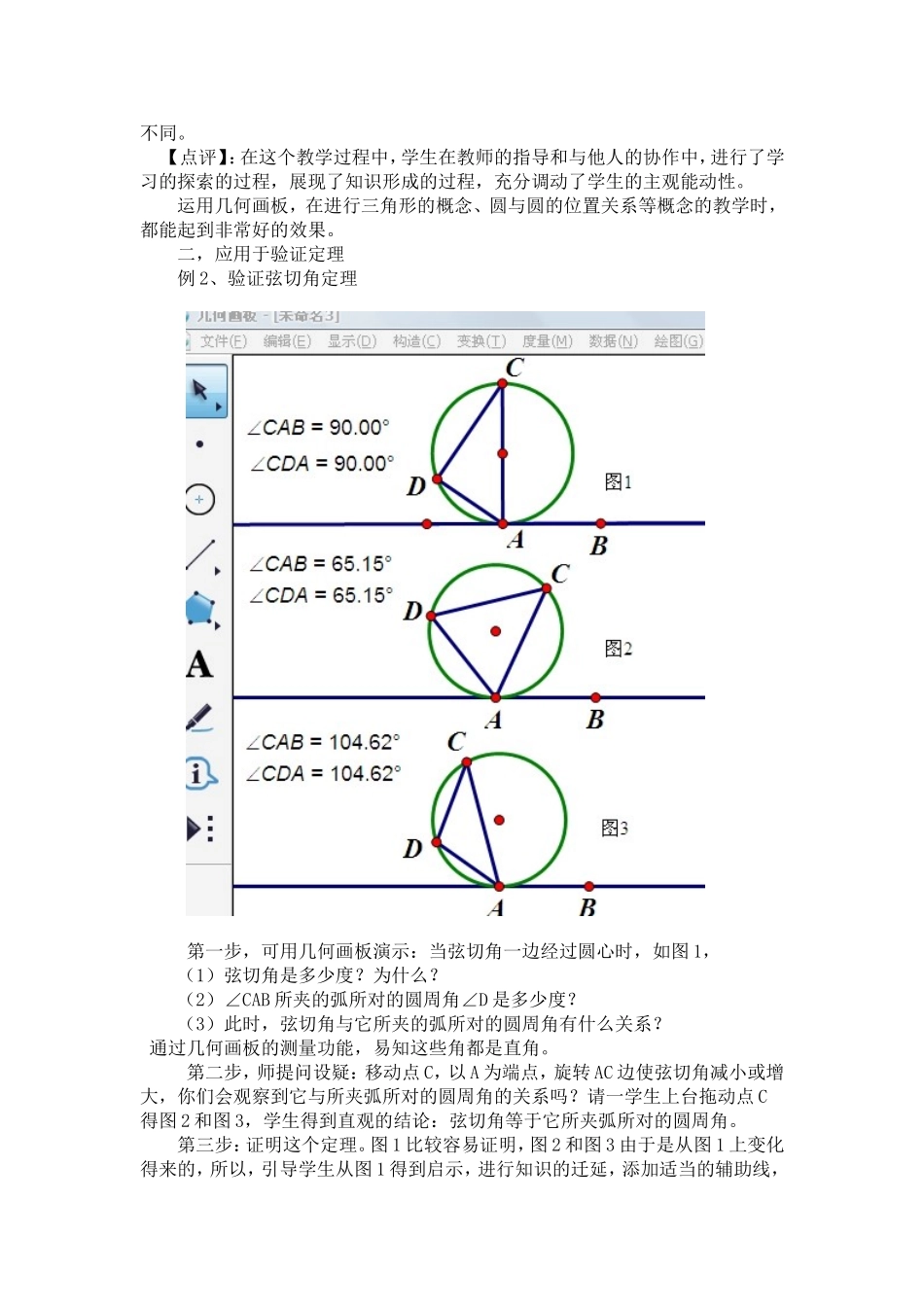
浅谈现代教育技术与高效数学课堂的有机整合————例谈几何画板的运用江苏省启东市开发区中学(226200)朱正英新课程标准要求数学课程的设计与实施应重视运用现代信息技术,把现代信息技术作为学生学习数学和解决问题的强有力的工具,使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去。正确地借助信息技术应用于数学教学做到现代教育技术与高效数学课堂的有机整合,有利于激发学生学习兴趣和积极性,有利于展现知识的形成过程,促进学生理解数学知识,有利于学生创造能力和动手实践能力的培养。几何画板被称之为21世纪的动态几何,它能使图形在运动中保持几何关系不变,深入几何的精髓。在数学教学中,它的动态性、形象性、可操作性受到众多师生的喜爱,它给学生提供了可自主探索的平台,使学生对数学产生较浓厚的兴趣,尤其能增强学生对一些含有动点的难点问题的解题信心。在当前大力开展素质教育的情形下,把几何画板交给学生无异于交给学生一把金钥匙,实现了现代教育技术与高效课堂的有机整合,是一件特别有意义的事。下面谈谈我在初中数学教学中运用几何画板进行教学的实例,与大家分享。一、应用于揭示概念例1、直角三角形中正弦的概念在∠FAG的一边AF上取不同的点B、D,分别作另一边AG的垂线,计算∠FAG的对边与斜边的比值。师:观察这个角的对边与斜边的比值,你有什么发现?生:发现一个固定的角的对边与斜边的比值也是固定的。师:谁愿意上来再取一个点试试,这个规律还存在吗?生争先恐后的举手,要求上台实践操作,师请一生上台演示,验证上述结论。这样就很容易的得出了一个锐角的正弦的概念。师拖动点A,∠FAG的大小不停的改变,师:随着角度的改变,∠FAG的对边与斜边的比值将会怎样?生:角度改变了,角的对边与斜边的比值也随着改变。不同锐角的正弦值也不同。【点评】:在这个教学过程中,学生在教师的指导和与他人的协作中,进行了学习的探索的过程,展现了知识形成的过程,充分调动了学生的主观能动性。运用几何画板,在进行三角形的概念、圆与圆的位置关系等概念的教学时,都能起到非常好的效果。二,应用于验证定理例2、验证弦切角定理第一步,可用几何画板演示:当弦切角一边经过圆心时,如图1,(1)弦切角是多少度?为什么?(2)∠CAB所夹的弧所对的圆周角∠D是多少度?(3)此时,弦切角与它所夹的弧所对的圆周角有什么关系?通过几何画板的测量功能,易知这些角都是直角。第二步,师提问设疑:移动点C,以A为端点,旋转AC边使弦切角减小或增大,你们会观察到它与所夹弧所对的圆周角的关系吗?请一学生上台拖动点C得图2和图3,学生得到直观的结论:弦切角等于它所夹弧所对的圆周角。第三步:证明这个定理。图1比较容易证明,图2和图3由于是从图1上变化得来的,所以,引导学生从图1得到启示,进行知识的迁延,添加适当的辅助线,加以证明。【点评】:这一运动变化过程,我给学生充分的探究时间,使学生不仅体会到知识的发现过程,而且进一步领会到规律成立的依据,使学生的认识水平进入又一个崭新的高度。除了弦切角定理,初中数学中的许多性质、定理都可以使用几何画板来验证如三角形内角和定理、平行四边形的性质定理、角平分线的性质定理及判定定理等等。三、应用于展现图形的变换过程(1)平移变换:如全等三角形的平移变换中,通过几何画板的动画演示,学生很直观地找到全等三角形的对应边,对应角,理解平移的方向和距离等概念。(2)翻折变换:动画演示等腰三角形沿对称轴翻折后,对称轴两旁的部分能完全重合,让学生通过观察图形,得出等腰三角形的一系列性质。(3)旋转变换:通过动画演示,学生很容易的理解旋转中心和旋转角的概念,丰富学生的空间想象能力,化抽象为具体,帮助学生突破难点。例3等边三角形ABC中一点0,AO=3,CO=4,∠AOC=150°,求BO的长。首先,我运用几何画板设置了动画,鼠标点击动画角度参数按钮,学生们就会观察到屏幕上出现的△BOC绕点C旋转到△ADC,接着,教师让学生分组讨论:在这个变换过程中,你发现了什么?生1:我发现旋转过程中的旋转中心是点C,旋转角是60°生2:我发现图中相等的线段有BO=AD,CO=CD,BC...