南通地区数学学科球的表面积和体积VIP免费

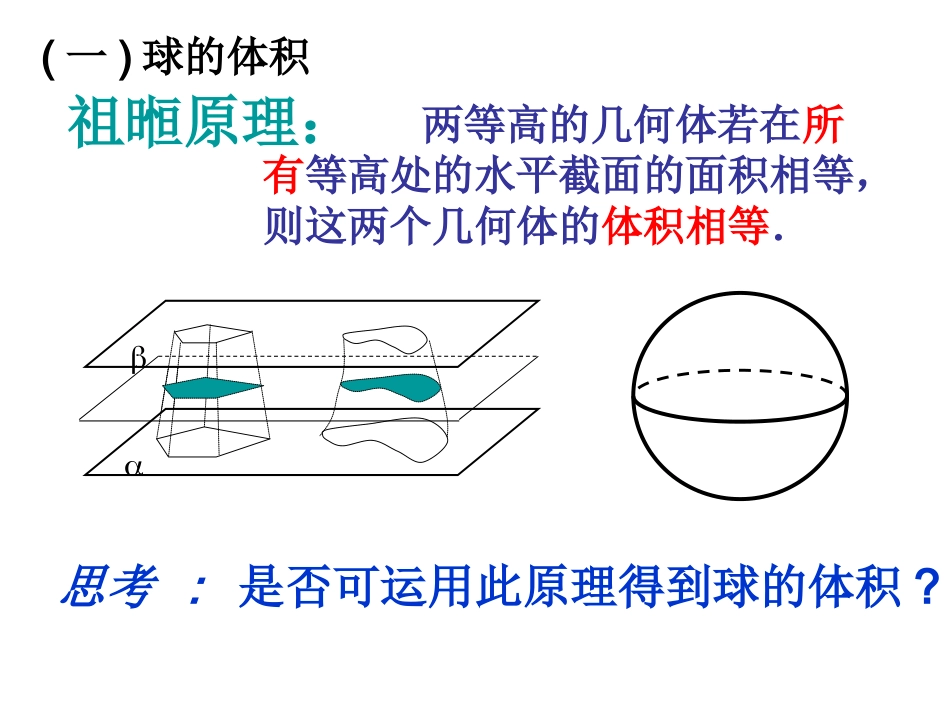
球的体积与表面积复习１．柱体的体积公式２．锥体的体积公式３．台体的体积公式V柱体=shV锥体=1sh3V台体=1h(s+ss'+s')3这些公式推导的依据是什么？(一)球的体积两等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等．祖暅原理：思考:是否可运用此原理得到球的体积?R观察：半球的体积与底面积相等的旋转体体积对比结论：°ëÇòԲ׶ԲÖùVVV(一)球的体积Rrlo因此S圆=2r=()22lR=2R2llloll设球的半径为R,截面半径为r,平面与截面的距离为那么r=22lRl(一)球的体积Rrloo因此S圆=2r=()22lR=2R2l设球的半径为R,截面半径为r,平面与截面的距离为那么r=22lRl(一)球的体积olRrlooO1LPNKlBO2S圆环=2R2l圆环面积S圆=S圆环因此S圆=2r=()22lR=2R2l设球的半径为R,截面半径为r,平面与截面的距离为那么r=22lRl(一)球的体积RrlooO1LPNKlBO2(一)球的体积根据祖暅原理，这两个几何体的体积相等，即=V球=312RRRR2323R21所以V球=343R探究（二）球的表面积分割求近似值化为精确值无限分割逼近精确值R球面球RSV31探究（二）球的表面积)(3131313131321321nnSSSSRRSRSRSRSV球当n足够大时24RS球面准锥体iSiViSiV例1、(1)钢球直径是5cm,则它的体积为。表面积为。三、公式的应用225cm36125cm（2）某街心花园有许多钢球,每个钢球重145kg，并且外径等于50cm，试根据以上数据，判断钢球是实心的还是空心的．如果是空心的，请你计算出它的内径（钢的密度是7.9g/cm3，π取3.14，结果精确到1cm）．解：由于外径为50cm的钢球的质量为：街心花园中钢球的质量为145000g，而145000<517054，所以钢球是空心的，34507.9517054()32g三、公式的应用解得：答：钢球是空心的．其内径约为45cm．3345047.9145000323x311239.42,x22.4.x设其内径是2xcm，那么球的质量为：所以2x=44.8≈45（3）如图是一个奖杯的三视图,单位是cm，试画出它的直观图，并计算这个奖杯的体积.(精确到0.01cm)86618515151111x/y/z/三、公式的应用解：这个奖杯的体积为V=V正四棱台+V长方体+V球其中V正四棱台2215(151511+11)851.6673V长方体=6×8×18=864V球=3433所以这个奖杯的体积为V≈1828.76（cm3）三、公式的应用097.113例2、（1）把半径为3cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸制作纸盒?球内切于正方体分析：用料最省时,球与正方体有什么位置关系?两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.三、公式的应用例2、（2）把正方体的纸盒装入半径为4cm的球状木盒里,能否装得下?分析：半径为4cm的球状木盒能装下的最大正方体与球盒有什么位置关系？球外接于正方体两个几何体相接:一个几何体的所有顶点都在另一个几何体的表面上。三、公式的应用OABCO例３已知过球面上三点A、B、C的截面到球心O的距离等于球半径的一半，且AB=BC=CA=２cm，求球的体积，表面积．解：如图，设球O半径为R，截面⊙O′的半径为r，r332AB2332AO是正三角形，ABCROO,2.34R.96491644S2R,)332()2R(R222OABCO,,222AOOOOAAOORt中解：在;81256)34(343433RV例３.已知过球面上三点A、B、C的截面到球心O的距离等于球半径的一半，且AB=BC=CA=２cm，求球的体积，表面积．练习：（1）一个正方体内接于半径为R的球内,则正方体的体积为。（2）棱长为a的正方体内有一个球与这个正方体的12条棱都相切，则这个球的表面积为。三、公式的应用(3)有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,则这三个球的体积之比为.表面积之比为.2.一个正方体的顶点都在球面上,它的棱长是4cm,这个球的体积为＿＿＿cm3.83323.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________.1.球的直径伸长为原来的2倍,体积变为原来的＿倍.练习一课堂练习33:22:14.若两球体积...