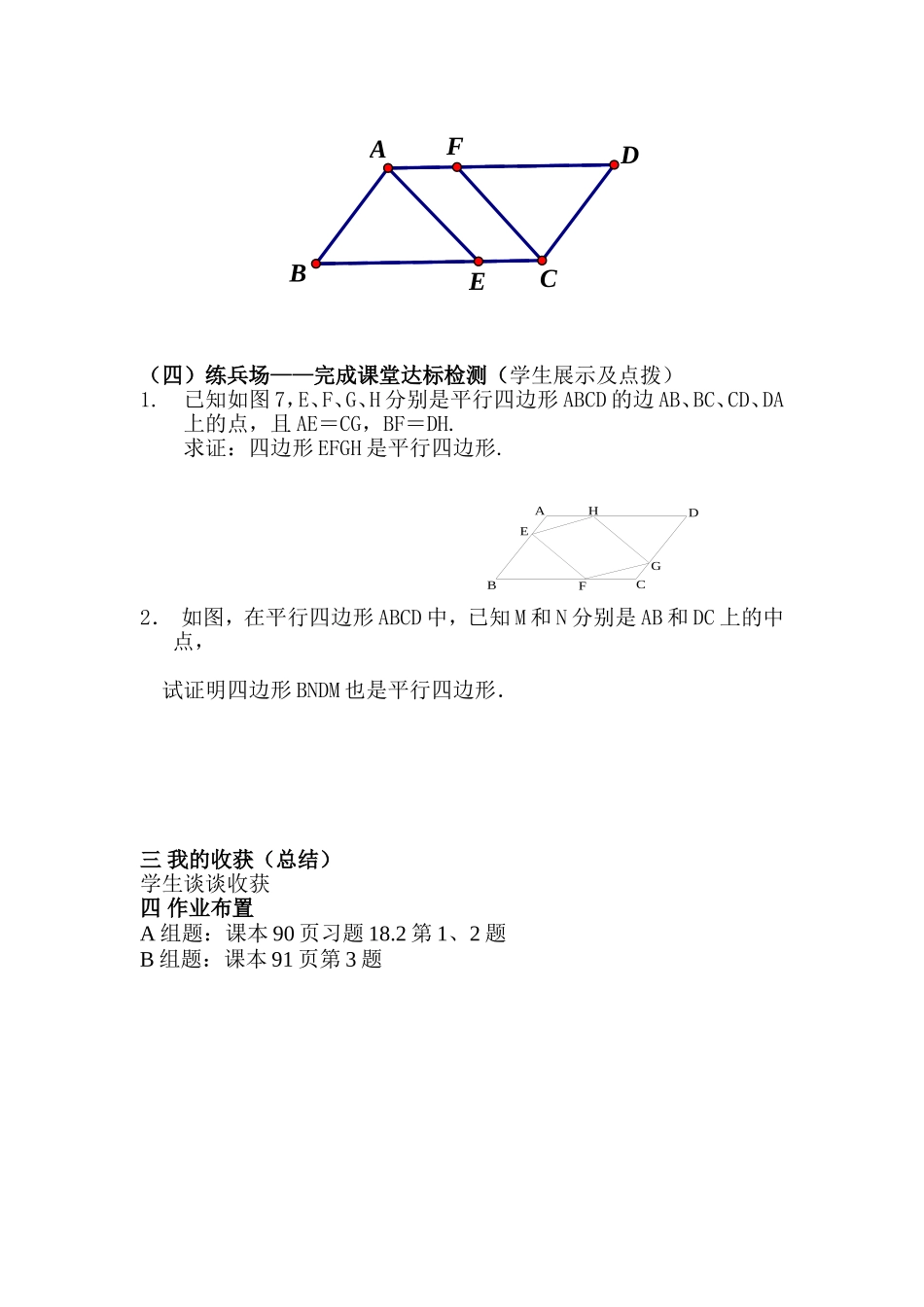
§18.2平行四边形的判定(第一课时)【学习目标】1.从边的角度探索并掌握平行四边形的两个判定定理,并能进行有关的论证和计算;2.经历平行四边形判别条件的探索过程,逐步掌握说理的基本方法;会应用平行四边形的判定定理,能合理清晰地表达自己的思维过程.【重点】平行四边形的判定定理;【难点】掌握平行四边形的性质和判定的区别及熟练应用.【学习过程】一知识回顾平行四边形的定义:两组对边分别平行的四边形是平行四边形.平行四边形的性质:边——平行四边形的对边平行且相等;角——平行四边形的对角相等,邻角互补;对角线——平行四边形的对角线互相平分.我们从边、角、对角线三个方面描述了平行四边形的性质,同样我们也可以从这三方面来探索平行四边形的判定.(引出课题,板书课题)有目标,学习就有方向.(引出学习目标)二授新(一)出示学习目标,学生齐读学习目标.(二)今天我们先从边这个角度研究平行四边形的判定方法.从“边”上我们已经知道的判定方法是定义——两组对边分别平行的四边形是平行四边形,那么,从边上还有哪些条件可以证明一个四边形是平行四边形呢?请同学们大胆的猜想。请同学们带着这个问题根据学习目标交流导学案中的“自主学习和合作探究”1.自主学习精读一遍教材P81-P84用红色笔进行勾画;在针对预习设计第二次阅读教材,解答导学案中的问题;找出自己的疑惑和需要讨论的问题,准备课堂讨论质疑.【知识回顾】什么叫平行四边形?平行四边形有什么性质?【预习设计】阅读课本回答下列问题怎样判定一个四边形是平行四边形呢?我们可以根据平行四边形的原始定义:加以判定。那么,是否存在其他的判定方法呢?由平行四边形的性质“平行四边形的两组对边分别相等”和“平行四边形的对边平行且相等”逆向思考,互换题设和结论,可以得到:和你认为这两个猜想成立吗?2.合作探究【探究一】命题“两组对边分别相等的四边形是平行四边形”已知:如图,在四边形ABCD中,AD=BC,AB=DC.求证:四边形ABCD是平行四边形.归纳平行四边形的判定理:。用几何语言表示判定定理:【探究二】命题“一组对边平行且相等的四边形是平行四边形”已知:如图20.1.4,在四边形ABCD中,AB∥CD且AB=CD.求证:四边形ABCD是平行四边形.归纳平行四边形的判定理:。用几何语言表示判定定理:(三)展示点拨1.让学生谈谈自己的猜想.2.让学生验证猜想.(让学生上黑板板书猜想过程)3.学生评价,老师点拨.4.知识归纳:平行四边形的方法目前有哪几种?答案:定义——两组对边分别平行的四边形是平行四边形;判定定理(一)——两组对边分别相等的四边形是平行四边形;判定定理(二)——一组对边平行且相等的四边形是平行四边形.5.例题讲解例:如图,在□ABCD中,E、F分别是对边BC和AD上的两点,且AF=CE,求证:四边形AECF是平行四边形.(让学生用不同的方法来解决问题)ADBCFE(四)练兵场——完成课堂达标检测(学生展示及点拨)1.已知如图7,E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.2.如图,在平行四边形ABCD中,已知M和N分别是AB和DC上的中点,试证明四边形BNDM也是平行四边形.三我的收获(总结)学生谈谈收获四作业布置A组题:课本90页习题18.2第1、2题B组题:课本91页第3题ABCDFHEG