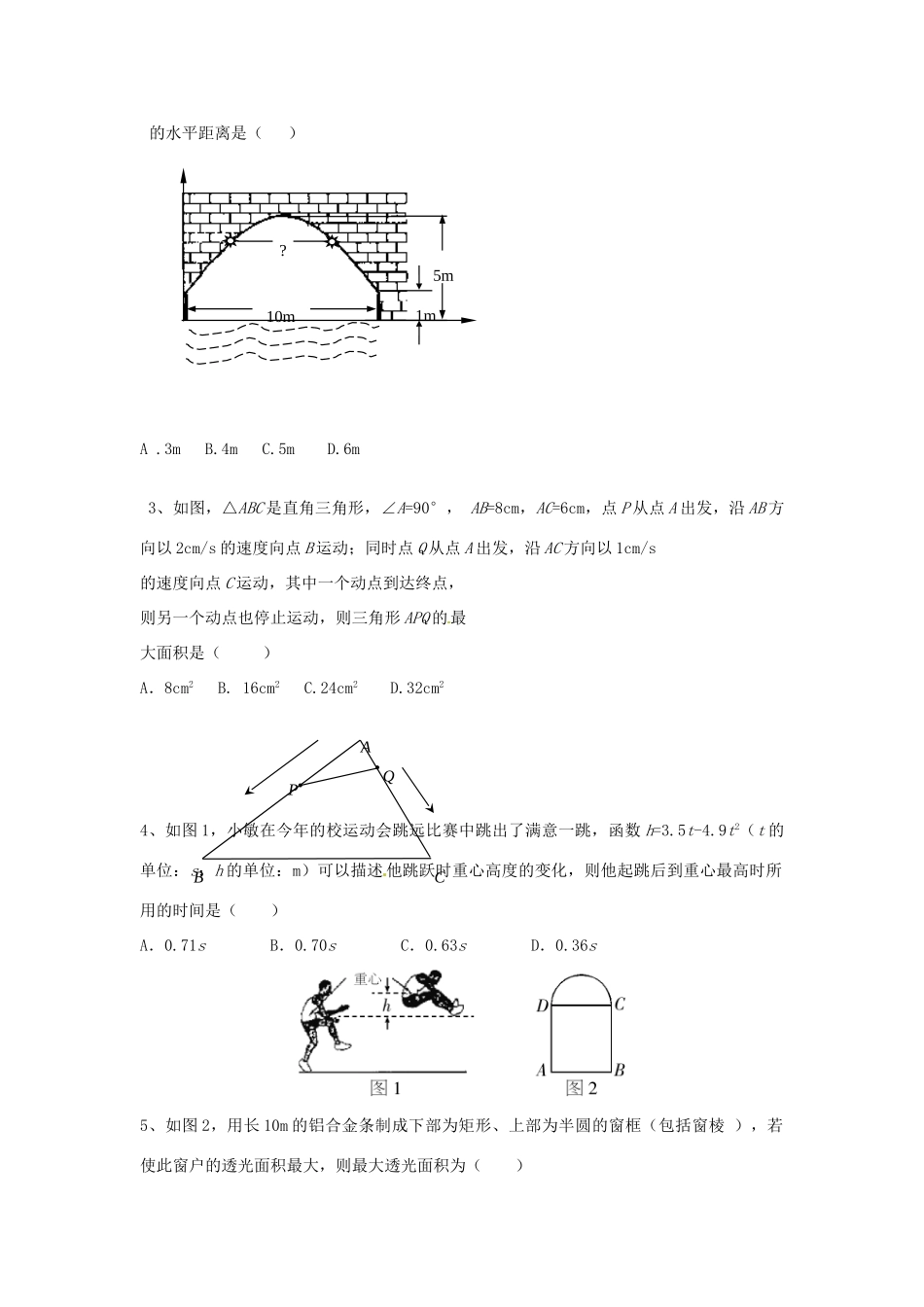
26.3实际问题与二次函数(2)习题1、用铝合金型材做一个形状如图(1)所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图(2)所示。观察图象,当x=时,窗户透光面积最大。2、隧道的截面是抛物线,且抛物线的解析式为y=,一辆车高3m,宽4m,该车通过该隧道。(填“能”或“不能”)3、如图所示是一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数图象。现观察图象,铅球推出的距离是_____m。4、有一个抛物线形拱桥,其最大高度为16米,跨度为40米,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的解析式为。二、选择题1、某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物的厚度忽略不记)()。A、5.1米B、9米C、9.1米D、9.2米2、图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间5m1m10m?的水平距离是()A.3mB.4mC.5mD.6m3、如图,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm,点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是()A.8cm2B.16cm2C.24cm2D.32cm24、如图1,小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h=3.5t-4.9t2(t的单位:s;h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是()A.0.71sB.0.70sC.0.63sD.0.36s5、如图2,用长10m的铝合金条制成下部为矩形、上部为半圆的窗框(包括窗棱),若使此窗户的透光面积最大,则最大透光面积为()ABCPQA.50πB.C.D.◎综合应用拓展1、某种鲜花的成本价为每盆12元,在销售中每盆鲜花售价(元)与每日销售量(盆)之间的函数关系如图4所示.(1)求y(盆)与x(元)的函数关系式;(2)每盆鲜花的售价定为多少时每日可获得最大利润,最大利润是多少?2、如图4所示,一座抛物线型拱桥,桥下水面宽度是4m,拱高是2m,当水面下降1m后,水面宽度是多少?(,结果保留0.1m)图43、有一座抛物线形桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.(1)在如图5所示的直角坐标系中,求出该抛物线的函数关系式;(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),求出d(表示为关于h的函数关系式);(3)设正常水位时桥下的水深2m,为保证过往船只顺利通行,水面宽度至少要有18m,求出这时水深多少米?4、已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,(1)AC=______;(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数表达式为S=_____.(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?(4)总面积S取最大值或最小值时,点C在AB的什么位置?