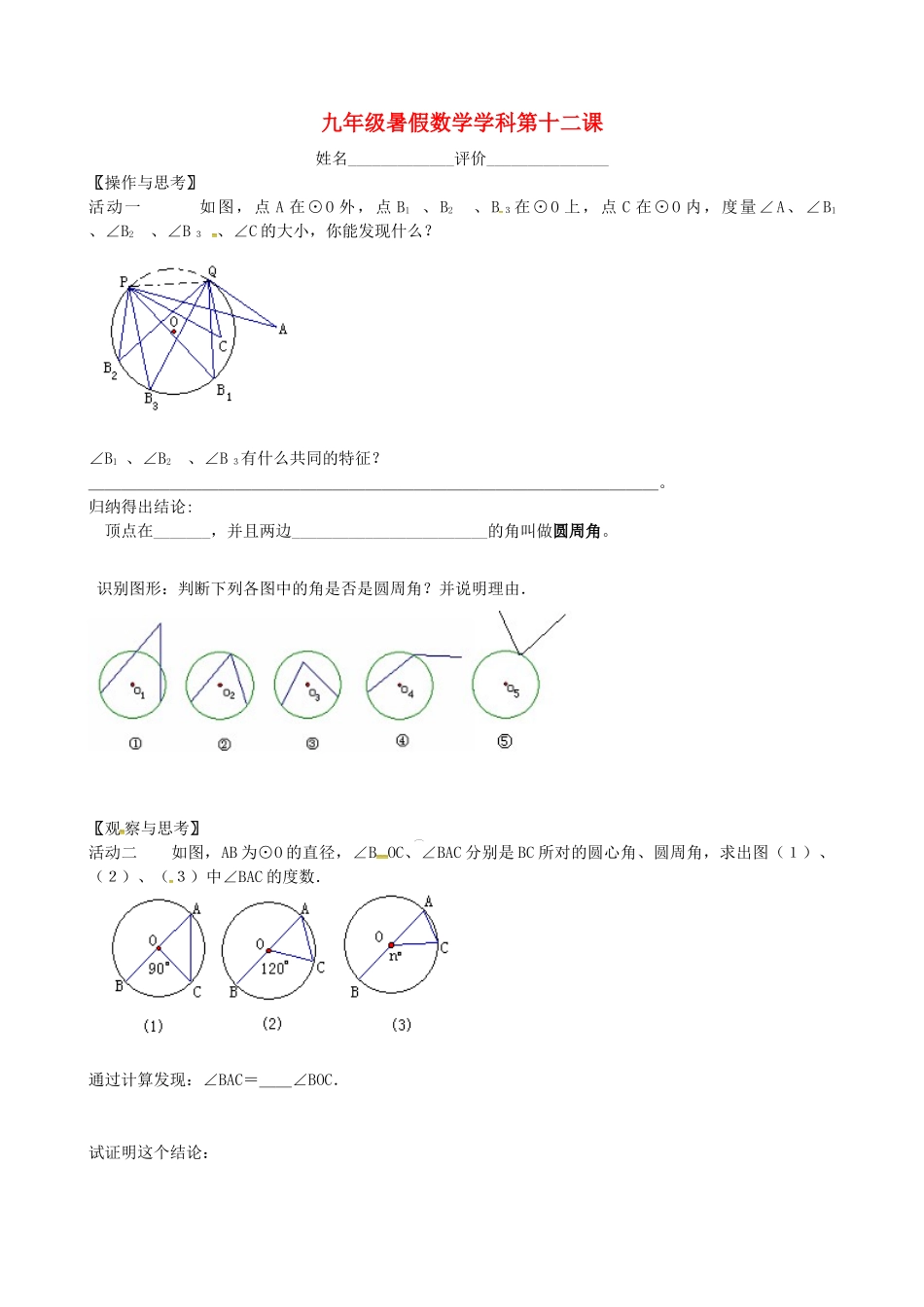
九年级暑假数学学科第十二课姓名_____________评价_______________〖操作与思考〗活动一如图,点A在⊙O外,点B1、B2、B3在⊙O上,点C在⊙O内,度量∠A、∠B1、∠B2、∠B3、∠C的大小,你能发现什么?∠B1、∠B2、∠B3有什么共同的特征?___________________________________。归纳得出结论:顶点在_______,并且两边________________________的角叫做圆周角。识别图形:判断下列各图中的角是否是圆周角?并说明理由.〖观察与思考〗活动二如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC所对的圆心角、圆周角,求出图(1)、(2)、(3)中∠BAC的度数.通过计算发现:∠BAC=__∠BOC.试证明这个结论:·O·O·O活动三〖思考与探索〗1.如图,BC所对的圆心角有多少个?BC所对的圆周角有多少个?请在图中画出BC所对的圆心角和圆周角,并与同学们交流。2.思考与讨论(1)观察上图,在画出的无数个圆周角中,这些圆周角与圆心O有几种位置关系?请在下图中画出这几种位置关系.(1)(2)(3)(2)设BC所对的圆周角为∠BAC,除了圆心O在∠BAC的一边上外,圆心O与∠BAC还有哪几种位置关系?对于这几种位置关系,结论∠BAC=12∠BOC还成立吗?试证明之.通过上述讨论发现:___________________________________OCBAFODABCE_______。〖解决问题〗例1、如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。例2:如图,OA、OB、OC都是圆O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.〖达成与迁移〗课内练习练习:120页练习2、31、如图6,已知∠ACB=20º,则∠AOB=_____,∠OAB=.2、如图7,已知圆心角∠AOB=1000,则∠ACB=_______。课外作业ͼ6OBACDOCBA图1DOCBA图2EDOCBA第3题1、填空题(1)如图四边形ABCD内接于⊙O,∠BOC=100°,则∠A=°(2)如图,A、B、C是⊙O上三点,D是AB延长线上一点,∠CBD=65°,则∠AOC=°(3)如图,已知⊙O的弦AD、CB交于点E,的度数为60°,的度数为100°,则∠AEC=°2、选择题(1)半径为4cm,120°的圆心角所对的弦长为()(A)5cm;(B)cm;(C)6cm;(D)cm;(2)中华人民共和国国旗上的五角星的画法通常是先把圆五等分.然后连结五等分点而得(如图).五角星的每一个角的度()(A)30°(B)35°(C)36°(D)37°3.如图,AC是⊙O的直径,BD是⊙O的弦,EC∥AB,交⊙O于E。图中哪些与12∠BOC相等?请分别把它们表示出来.4.一条弦分圆1:4两部分,求这弦所对的圆周角的度数?