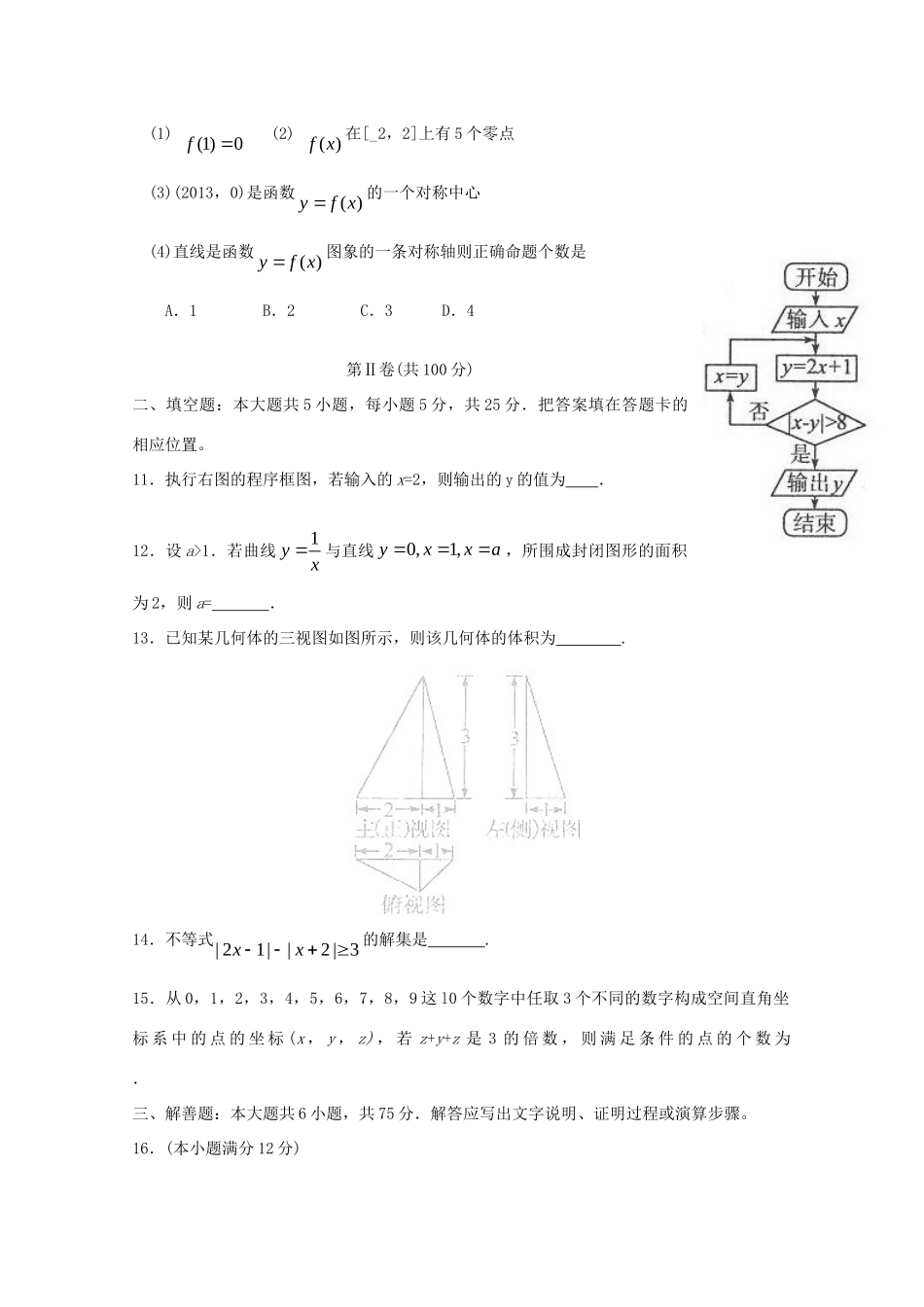
德州市高中三年级模拟检测数学(理科)试题2014.3本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷1—2页.第Ⅱ卷3—4页,共150分。测试时间120分钟。注意事项:选择题为四选一题目,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。第I卷(共50分)一、选择题:本大题共10小题。每小题5分,共50分把正确答案涂在答题卡上。1.已知全集为R,集合A={1|()12xx},B={|2xx},RABð=A.[0,2)B.[0,2]C.(1,2)D.(,2]2.设复数21izi,则复数2z的实部与虚部的和为A.0B.2C.2D.43.对具有线性相关关系的变量x,y,有一组观测数据(ix,iy)(i=1,2,…,8),其回归直线方程是:16yxa,且12381238...3(...)6xxxxyyyy,则实数a的值是A.116B.18C.14D.11164.若a,b均为实数,且方程222(1)20xaxbb无实根,则函数()logabyx是增函数的概率是A.1142B.142C.12D.11245.ABC中内角A,B,C的对边分别是a,b,c.若223sin23sinabbcCB,,则A=A.56B.23C.3D.66.已知变量x,y满足约束条件11xyxyxa,若25xy恒成立,则实数a的取值范围为A.(-,-1]B.[-1,+)C.[-1,1]D.[-1,1)7.函数sin,[,]yxxx的大致图象是8.已知双曲线2222:1(0,0)xyCabab的焦距为25,抛物线21116yx与双曲线C的渐近线相切,则双曲线C的方程为A.22182xyB.22128xyC.2214yxD.2214xy9.已知平面内点A,B,O不共线,APOAOB�,则A,P,B三点共线的必要不充分条件是A.=B.||=||C.=-D.=1-10.已知函数()yfx是定义在R上的奇函数,对xR都有(1)(1)fxfx成立,当(0,1]x且12xx时,有2121()()0fxfxxx。给出下列命题(1)(1)0f(2)()fx在[_2,2]上有5个零点(3)(2013,0)是函数()yfx的一个对称中心(4)直线是函数()yfx图象的一条对称轴则正确命题个数是A.1B.2C.3D.4第Ⅱ卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置。11.执行右图的程序框图,若输入的x=2,则输出的y的值为.12.设a>1.若曲线1yx与直线0,1,yxxa,所围成封闭图形的面积为2,则a=.13.已知某几何体的三视图如图所示,则该几何体的体积为.14.不等式|21||2|3xx的解集是.15.从0,1,2,3,4,5,6,7,8,9这l0个数字中任取3个不同的数字构成空间直角坐标系中的点的坐标(x,y,z),若z+y+z是3的倍数,则满足条件的点的个数为.三、解善题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤。16.(本小题满分12分)已知函数1()cos()cos()3sincos334fxxxxx(I)求函数()fx的最小正周期和最大值;(II)若1(),(,)12342f,求sin2的值.17.(本小题满分12分)在一次综合知识竞赛中,有两道填空题和两道解答题,填空题每题5分,解答题每题10分,某参赛者答对填空题的概率都是34,答对解答题的概率都是23,解答备题的结果是相互独立的。(I)求该参赛者恰好答对一道题的概率;(II)求该参赛者的总得分X的分布列及数学期望E(X)18.(本小题满分12分)在直角梯形ABCD中,ADC=90o,CD//AB,AB=4,AD=CD=2,M为线段AB的中点,将△ADC沿AC折起,使平面ADC平面ABC,得几何体D—ABC。(I)求证:BC平面ACD;(II)求二面角A—CD—M的余弦值。19.(本小题满分l2分)将数列{na}中的所有项按每一行比上一行多两项的规则排列成如下数表123456789,,,,,,aaaaaaaaa……已知表中的第一列数125,,aaa…构成一个等差数列,记为数列{nb},且2b=4,5b=10,表中每一行正中间一个数137,,aaa…构成数列{nc},其前n项和为nS.(I)求数列{nb}的通项公式;(II)若上表中从第2行开始,每一行中的数按从左到右的顺序均成等比数列,且公比是同一个正数,已知1952a,求nS.20.(本小题满分13分)设函数()ln()fxxaxaR(e=2.71828……是自然对数的底数).(I)判()fx断的单调性;(1I)当()0fx在(0,...