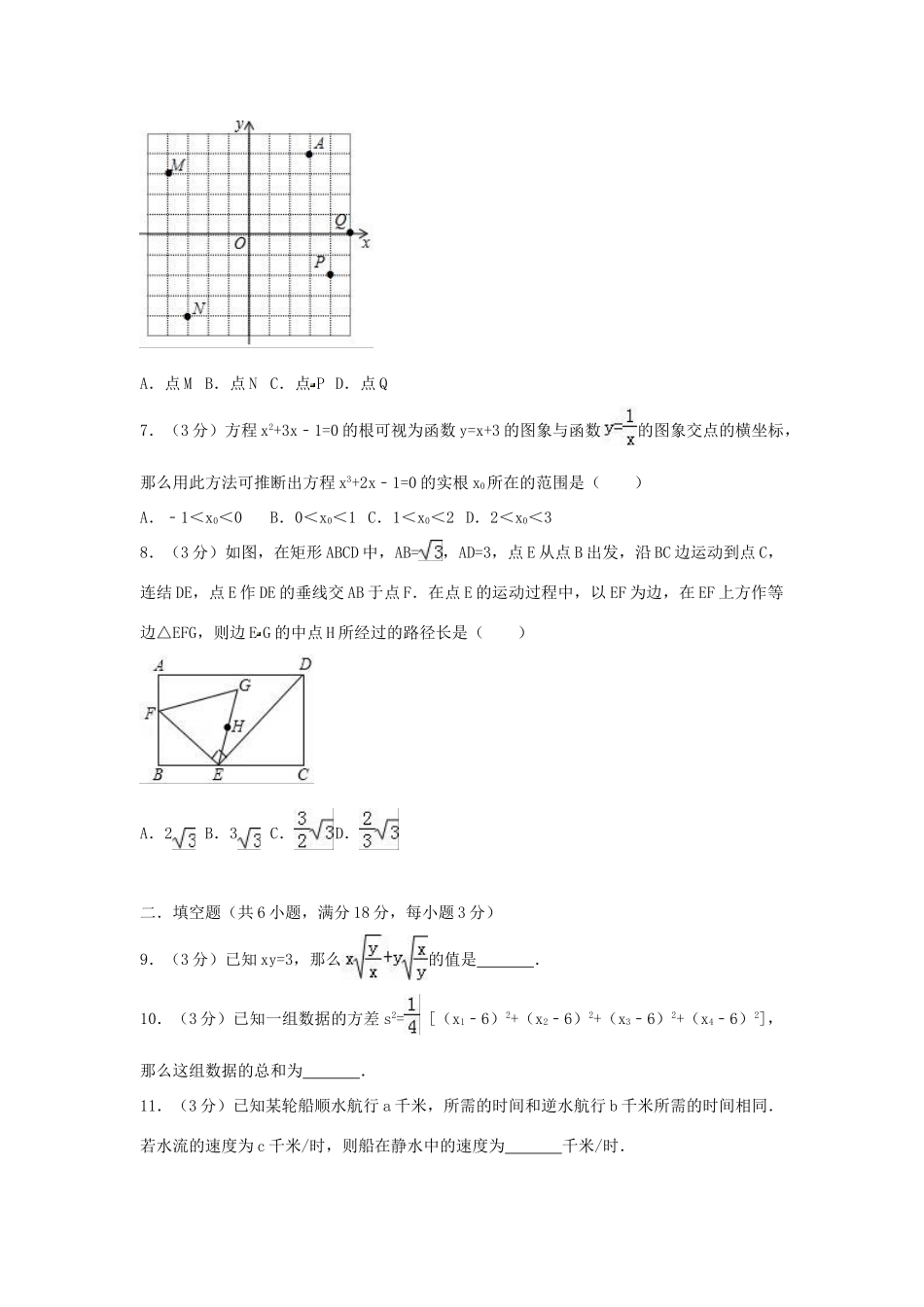
2017-2018学年山东省青岛市市北区九年级(下)期中数学模拟试卷(二)一.选择题(共8小题)1.当a、b互为相反数时(ab≠0),下列各式一定不成立的是()A.a+b=0B.|a|=|b|C.=﹣1D.=12.(3分)有以下图形:平行四边形、矩形、等腰三角形、线段、菱形,其中既是轴对称图形又是中心对称图形的有()A.5个B.4个C.3个D.2个3.已知某种型号的纸100张厚度约为1cm,那么这种型号的纸13亿张厚度约为()A.1.3×107kmB.1.3×103kmC.1.3×102kmD.1.3×10km4.(3分)平面上画着一些平行线,相邻的两条平行线之间的距离都为a,向此平面任投一长度为l(l<a)的针,求该针与平行线相交的概率.下列见解正确的是()A.可以用画树状图的方法求概率B.可以用列表的方法求概率C.可以用画树状图或列表的方法求概率,也可以用试验的方法估计其概率D.不能用画树状图或列表的方法求概率,可以用试验的方法估计其概率5.(3分)如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=50°,则∠ABC的度数为()A.20°B.25°C.40°D.50°6.(3分)如图,在平面直角坐标系xOy中,点A从(3,4)出发,绕点O顺时针旋转一周,则点A不经过()A.点MB.点NC.点PD.点Q7.(3分)方程x2+3x﹣1=0的根可视为函数y=x+3的图象与函数的图象交点的横坐标,那么用此方法可推断出方程x3+2x﹣1=0的实根x0所在的范围是()A.﹣1<x0<0B.0<x0<1C.1<x0<2D.2<x0<38.(3分)如图,在矩形ABCD中,AB=,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是()A.2B.3C.D.二.填空题(共6小题,满分18分,每小题3分)9.(3分)已知xy=3,那么的值是.10.(3分)已知一组数据的方差s2=[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],那么这组数据的总和为.11.(3分)已知某轮船顺水航行a千米,所需的时间和逆水航行b千米所需的时间相同.若水流的速度为c千米/时,则船在静水中的速度为千米/时.12.(3分)如图,ABCDE是正五边形,已知AG=1,则FG+JH+CD=.13.(3分)如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,AB=6cm,BC=10cm,点Q从点A出发以1cm/s的速度向点D运动,点P从点B出发以2cm/s的速度向C点运动,P、Q两点同时出发,其中一点到达终点时另一点也停止运动.若DP≠DQ,当t=s时,△DPQ是等腰三角形.14.(3分)一种树苗,栽种时高度约为80厘米,为研究它的生长情况,测得数据如下表:(1)此变化过程中是自变量,是因变量;(2)树苗高度h与栽种的年数n的关系式为;(3)栽种后后,树苗能长到280厘米.栽种以后的年数n/年高度h/厘米1105213031554180……三.解答题(共1小题,满分4分,每小题4分)15.(4分)在平面直角坐标系xOy中,点A(4,1),B(5,5),D(1,1).(1)在图1中找一点C,使△ABC为等腰直角三角形且满足∠BAC=90°,则点C坐标为.(2)在图2中画出以BD为边与△ABD全等的所有三角形.四.解答题(共9小题,满分74分)16.(8分)(1)计算与化简:÷×(2)解不等式4(3x﹣1)<5(2x+1)并把它的解集在数轴上表示出来.17.(6分)在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.18.(6分)如图,在一笔直的沿湖道路上有A、B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏东15°的方向,AB=4km.(1)求观光岛屿C与码头A之间的距离(即AC的长);(2)游客小明准备从观光岛屿C乘船沿甜回到码头A或沿CB回到码头B,若开往码头A、B的游船速度相同,设开往码头A、B所用的时间分别是t1、t2,求的值.(结果保留根号)19.(6分)某中学开展以“我最爱的职...