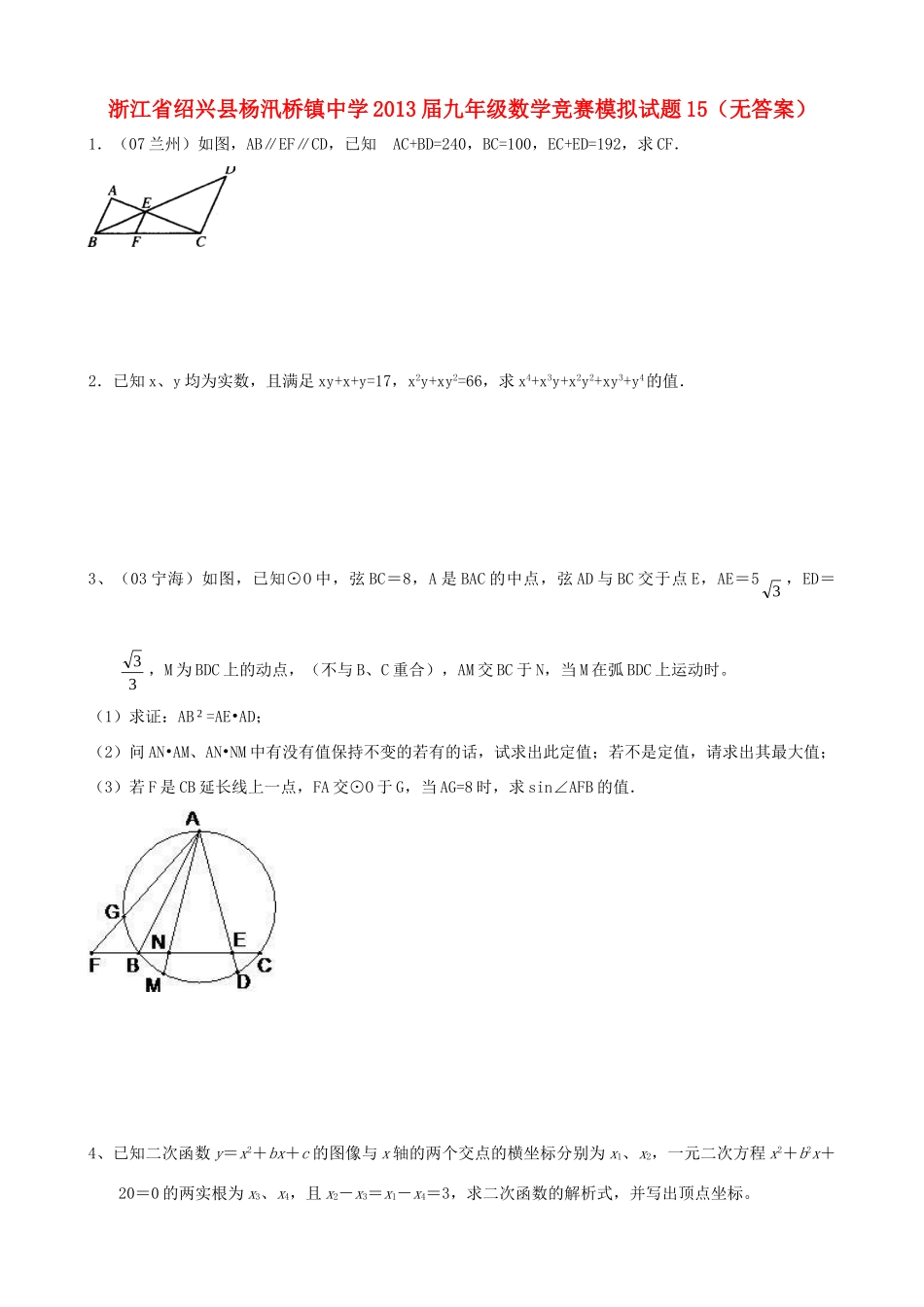
浙江省绍兴县杨汛桥镇中学2013届九年级数学竞赛模拟试题15(无答案)1.(07兰州)如图,AB∥EF∥CD,已知AC+BD=240,BC=100,EC+ED=192,求CF.2.已知x、y均为实数,且满足xy+x+y=17,x2y+xy2=66,求x4+x3y+x2y2+xy3+y4的值.3、(03宁海)如图,已知⊙O中,弦BC=8,A是BAC的中点,弦AD与BC交于点E,AE=53,ED=33,M为BDC上的动点,(不与B、C重合),AM交BC于N,当M在弧BDC上运动时。(1)求证:AB2=AE•AD;(2)问AN•AM、AN•NM中有没有值保持不变的若有的话,试求出此定值;若不是定值,请求出其最大值;(3)若F是CB延长线上一点,FA交⊙O于G,当AG=8时,求sin∠AFB的值.4、已知二次函数y=x2+bx+c的图像与x轴的两个交点的横坐标分别为x1、x2,一元二次方程x2+b2x+20=0的两实根为x3、x4,且x2-x3=x1-x4=3,求二次函数的解析式,并写出顶点坐标。5.(07慈溪)已知函数y=x2+(b-1)x+c(b,c为常数),这个函数的图象与x轴交于两个不同的点A(x1,0)和B(x2,0).若x1,x2满足x2-x1>1(1)求证:b2≥2(b+2c);(2)若t