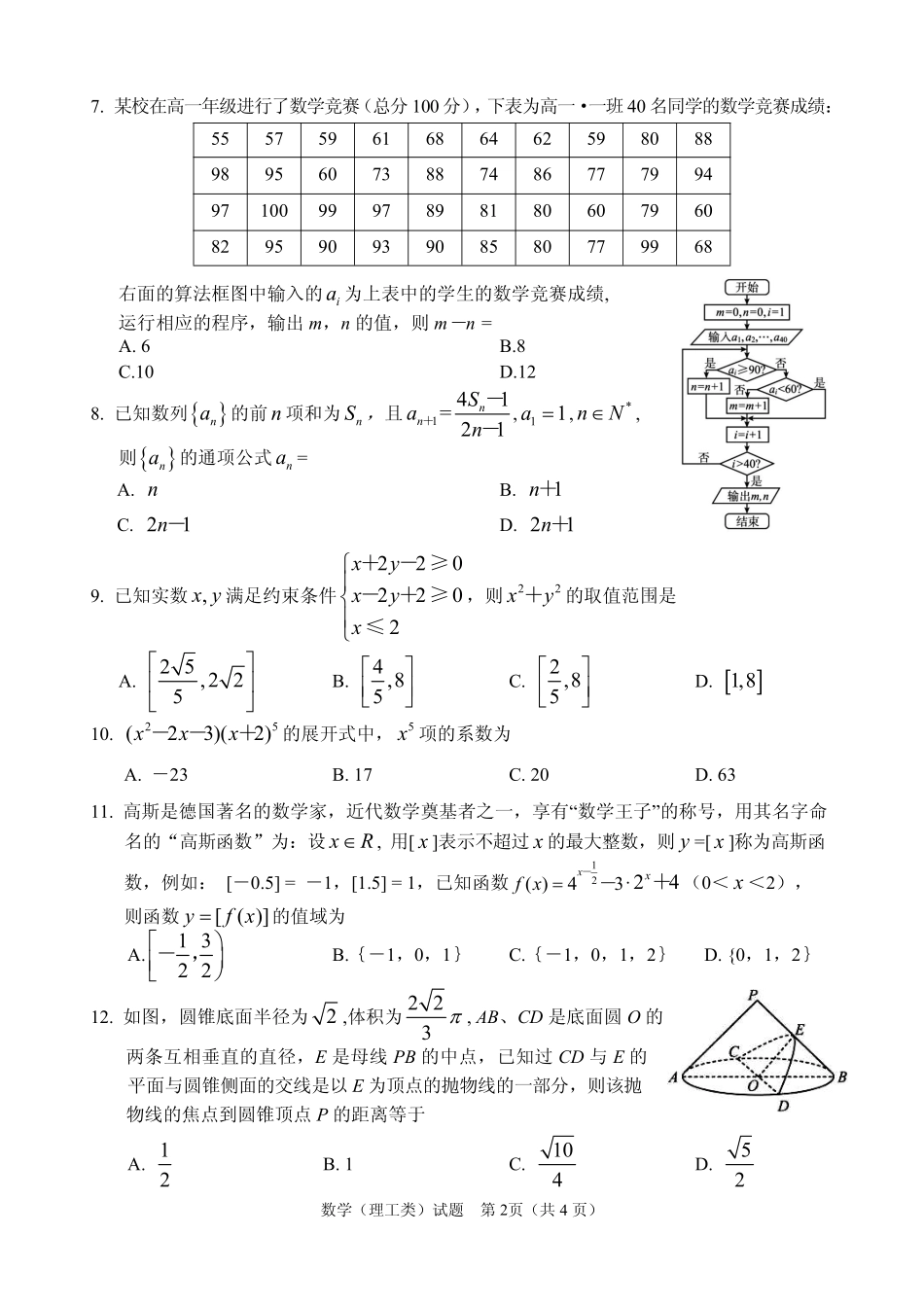
数学(理工类)试题第1页(共4页)眉山市高中2017级第二次诊断性考试数学(理工类)(考试时间:120分钟试卷满分:150分)注意事项:1.本次考试为“云考试”,答卷前考生务必将自己的姓名、准考证号填写在答题卷上.2.考生在试题作答、答题卷上传等方面按学校具体要求执行,规范作答.3.考试结束后,在规定时间内上传本次考试的答题卷给学校指定的教师.一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.集合A=10xx+>,B=2320xxx-+>,则ARðB=A.(-1,1)B.(1,2)C.[1,2]D.(-l,l)∪(l,+∞)2.已知向量a=(-m,4),b=(m,1)(其中m为实数),则“m=2”是“a丄b”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知复数z在复平面内对应的点的坐标为(-1,2),则下列结论正确的是A.z·i=2-iB.复数z的共轭复数是1-2iC.5zD.13i1i22z++4.已知函数31,0()(),0xxfxgxx是奇函数,则((1))gf的值为A.-10B.-9C.-7D.15.给出以下四个命题:1依次首尾相接的四条线段必共面;2过不在同一条直线上的三点,有且只有一个平面;3空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角必相等;4垂直于同一直线的两条直线必平行.其中正确命题的个数是A.0B.1C.2D.36.函数22()2cos(sincos)2fxxxx++的一个单调递增区间是A.[-4,4]B.[-8,38]C.[8,58]D.[58,98]数学(理工类)试题第2页(共4页)7.某校在高一年级进行了数学竞赛(总分100分),下表为高一·一班40名同学的数学竞赛成绩:555759616864625980889895607388748677799497100999789818060796082959093908580779968右面的算法框图中输入的ia为上表中的学生的数学竞赛成绩,运行相应的程序,输出m,n的值,则m-n=A.6B.8C.10D.128.已知数列na的前n项和为nS,且141=21nnSan+--,11a,*nN,则na的通项公式na=A.nB.1n+C.21n-D.21n+9.已知实数,xy满足约束条件2202202xyxyx+--+≥≥≤,则22xy+的取值范围是A.25,225B.4,85C.2,85D.1,810.25(23)(2)xxx--+的展开式中,5x项的系数为A.-23B.17C.20D.6311.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设xR,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,例如:[-0.5]=-1,[1.5]=1,已知函数12()43xfx--·24x+(0<x<2),则函数[()]yfx的值域为A.1322-,B.{-1,0,1}C.{-1,0,1,2}D.{0,1,2}12.如图,圆锥底面半径为2,体积为223,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离等于A.12B.1C.104D.52数学(理工类)试题第3页(共4页)AA1二、填空题:本题共4小题,每小题5分,共20分。13.已知等差数列na的前n项和为nS,且476=3aaa++,则9S=.14.如图,F1、F2分别是双曲线22221xyab-的左、右焦点,过F2的直线与双曲线C的两条渐近线分别交于A、B两点,若2FAAB,1FB·2FB=0,则双曲线C的离心率是______.15.已知正方体ABCD-A1B1C1D1棱长为2,点P是上底面A1B1C1D1内一动点,若三棱锥P-ABC的外接球表面积为414,则点P构成的图形围成的面积为.16.函数()xfxae与()1gxx--的图象上存在关于x轴的对称点,则实数a的取值范围为.三、解答题:共70分。解答应写出文字说明,证明过程或演算步骤。第17〜21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。(一)必考题:共60分。17.(本小题满分12分)如图,EFGH是矩形,△ABC的顶点C在边FG上,点A,B分别是EF,GH上的动点(EF的长度满足需求).设∠BAC=α,∠ABC=β,∠ACB=,且满足sinα+sinβ=sin(cosα+cosβ).(1)求;(2)若FC=5,CG=3,求53ACBC+的最大值.18.(本小题满分12分)在某社区举行的2020迎春晚会上,张明和王慧夫妻俩参...