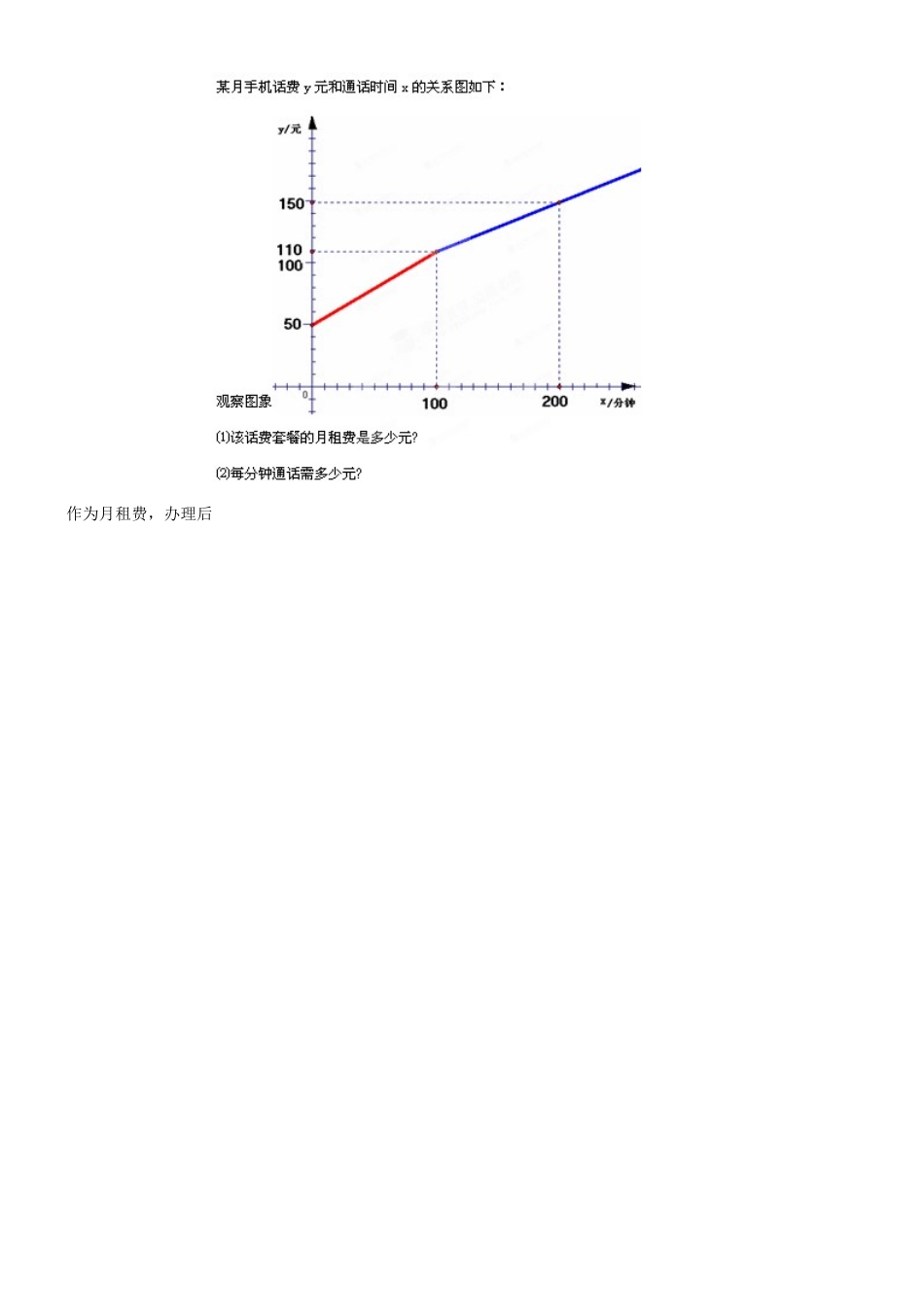
九年级数学下《一次函数》复习题【学习目标】熟练掌握一次函数的概念,并会正确判断是否是一次函数。能够画出一次函数的图像,并学会利用图像解决实际问题。理解一次函数的性质,并熟练应用解决相关问题。【学习过程】知识点1:一次函数概念一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。思考:y=kxn+b为一次函数的条件是什么?1、指数n=()2、系数k()例、若函数是一次函数,则m=___。有效训练11、下列函数中,不是一次函数的是()2、若函数是正比例函数,则n=()()决定一次函数图象与坐标轴交点的位置;()决定直线的倾斜方向。例、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是()有效训练21、有下列函数:①y=2x+1,②y=-3x+4,③y=0.5x,④y=x-6;函数y随x的增大而增大的是__________;函数y随x的增大而减小的是___________图象在第一、二、三象限的是________。2、直线y=(6-3m)x+(2n-4)不经过第三象限,则m、n的范围是_________。3、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第_______象限。知识点3:用待定系数法求函数解析式例、若函数y=3x+b经过点(2,-6),求函数的解析式。有效训练3直线y=kx+b的图像经过A(3,4)和点B(2,7)知识点4:函数问题与实际生活“五一”期间,天气晴朗,游人众多,交通比较拥挤。已知火车站托运行李费用与托运行李的重量关系如图所示。(1)当x=30时,y=_______;当x=_______,y=30。(2)你能确定该关系所在直线的函数解析式吗?(3)若你和家人出游,当货物少于千克,可免费托运。【堂清作业】:1、若函数是一次函数,则m=_______;2、如果一次函数y=kx+b的图像经过第一象限,且与y轴负半轴相交,那么k_____0,b_____0;(填写“>”、“=”、“<”);3、点P1(x1,y1),点P2(x2,y2)是一次函数y=-4x+3图像上的两点,且x1<x2,则:y1____y2(填写“>”、“=”、“<”);4、一次函数y=2x-2与x轴交点坐标为_______,与y轴的交点坐标为_______,与坐标轴围成的三角形的面积为_______;5.小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用30203040x(千克)y(元)作为月租费,办理后