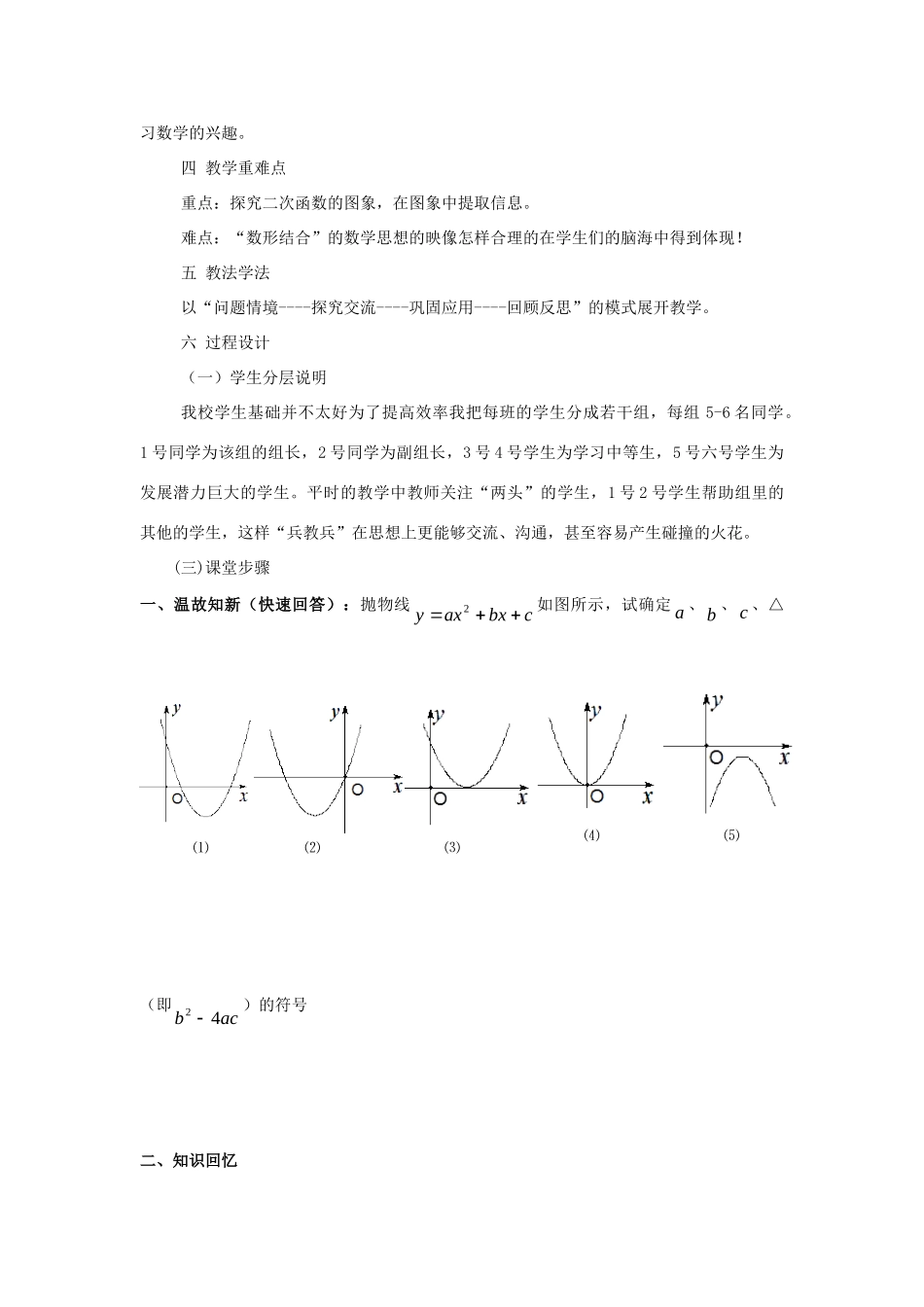
二次函数图象解题教学分析一教学分析:二次函数是学生继一次函数和反比例函数以后进一步学习的函数知识,是函数知识螺旋发展的重要环节起到承上启下的作用,为学生进入高中后进一步学习函数知识奠定基础二次函数是描述现实世界变量之间关系的重要数学模型。二次函数曲线—抛物线也是人们最为熟悉的曲线之一,复习二次函数主要有二次函数的概念、二次函数的图象和性质、以及二次函数的应用。二次函数的图象是它性质的直观体现,对了解和掌握二次函数的性质具有形象直观的优势。本节课主要是利用二次函数的图象,让学生学会观察图象,并能从图象中提炼出我们所需要的信息,来解决二次函数的具体问题。锻炼学生的师徒能力,培养学生的数形结合的数学思想,为中考做好贮备。二备课说明本节课的内容虽然并不多,但是它所反映的数学思想却是非常重要的。我国著名数学家华罗庚曾说过:“数形本是相绮依,焉能分作两边飞。数缺形时少直觉,形缺数时难入微。数形结合百般好,隔离分家万事休。”“数”与“形”反映了事物两个方面的属性。我认为数形结合就是数与形的对应关系,就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”、“以数解形”即通过抽象思维与形象思维的结合,可以是复杂问题简单化,抽象问题具体化,从而起到优化解题的目的。为了更好地完成本节课我决定采取分层教学来进行。对学生分组分层,采用“兵教兵”方式来进行。学生活动采用练习、讨论、讲解、回答等多种形式提高学生学习兴趣。课堂练习以及作业采用有区别的练习进行巩固所学习的知识,技能反馈教学效果。三教学目标(一)知识目标:会有函数图象提供的信息解决数学问题;(二)能力目标:建立“数形结合”的数学思想,并深刻体会“数形结合”的方法在解决数学问题中的作用。(三)情感价值目标:通过函数的知识灵活用于实际,让学生亲自体会到学习数学知识的价值,从而提高学习数学的兴趣。四教学重难点重点:探究二次函数的图象,在图象中提取信息。难点:“数形结合”的数学思想的映像怎样合理的在学生们的脑海中得到体现!五教法学法以“问题情境----探究交流----巩固应用----回顾反思”的模式展开教学。六过程设计(一)学生分层说明我校学生基础并不太好为了提高效率我把每班的学生分成若干组,每组5-6名同学。1号同学为该组的组长,2号同学为副组长,3号4号学生为学习中等生,5号六号学生为发展潜力巨大的学生。平时的教学中教师关注“两头”的学生,1号2号学生帮助组里的其他的学生,这样“兵教兵”在思想上更能够交流、沟通,甚至容易产生碰撞的火花。(三)课堂步骤一、温故知新(快速回答):抛物线cbxaxy2如图所示,试确定a、b、c、△(即acb42)的符号二、知识回忆⑴⑵⑶⑷⑸1、请你说出二次函数的两种形式:⑴一般式:⑵顶点式:2、根据下列条件求二次函数的解析式:⑴函数的图象经过点03,A、01,B、30,C⑵图象的顶点坐标为15,,且经过点53,三、慧眼识图:1、已知二次函数的图象如图所示。问题1:图中的点A、B、C的坐标分别是A(,)、B(,)、C(,)问题2:你能根据图中得到的信息,求出这个函数的解析式吗?2、(练笔)已知二次函数cbxaxy2的图象如图所示,求它的解析式。3、(挑战自我)已知抛物线的图象如图所示⑴求该抛物线的解析式;⑵分别求它关于x轴、y轴对称的抛物线的解析式。四、中考链接:相信你试一试,肯定会成功的!如图,是抛物线的一部分,你能写出一个符合条件的抛物线的解析式吗?五、学以致用要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为m1处达到最高,高度为m3,水柱落地处离池中心m3,水管应多长?