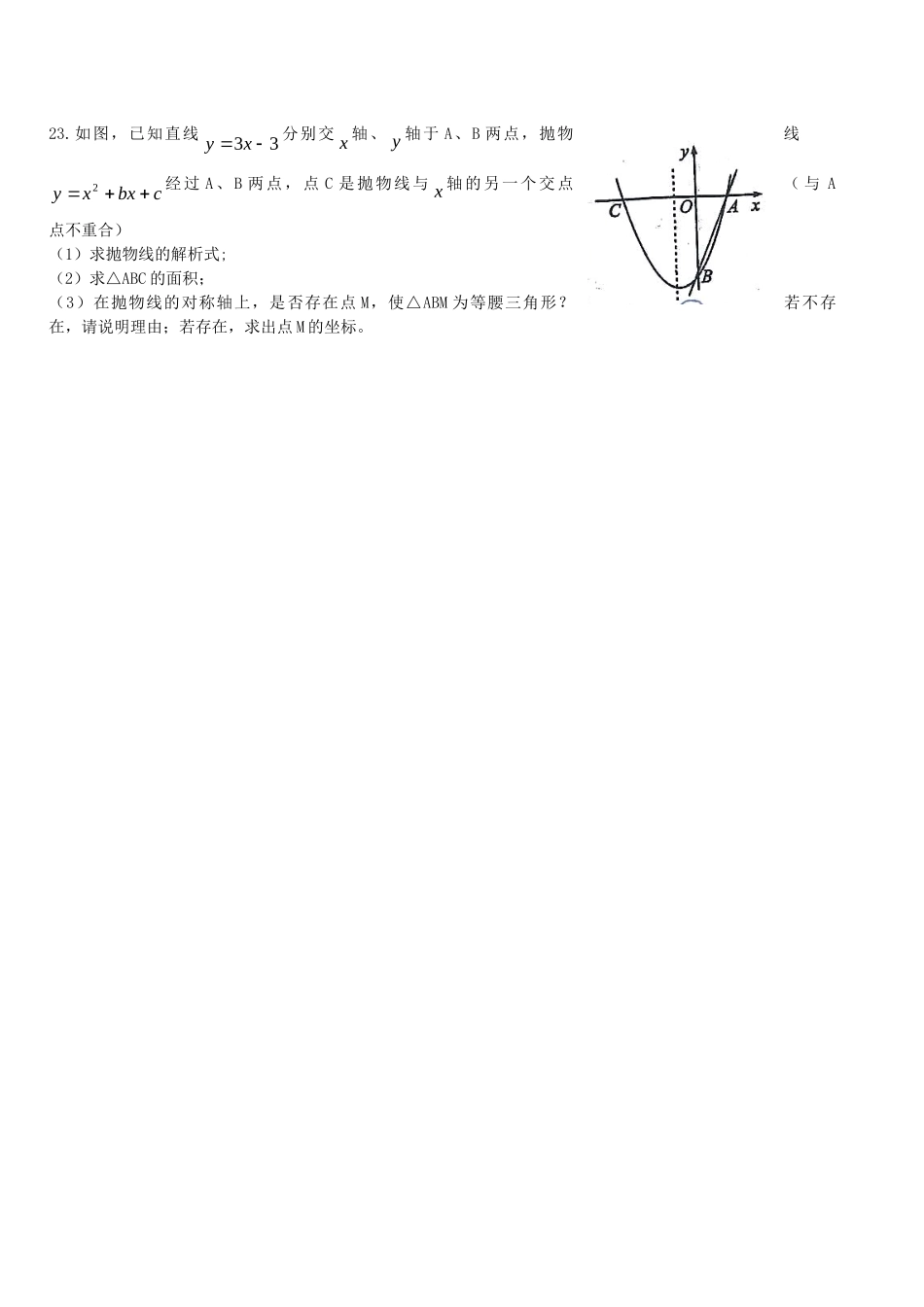
云南省腾冲县第六中学2014届九年级数学11月月考试题(考试时间:120分钟,满分:150分)一、填空题(每题3分,共30分)1、下列图案中,既是轴对称图形又是中心对称图形的是()2、下列方程中,是关于x的二元一次方程的是()A.012xxB.02cbxaxC.1)2)(1(xxD.02322yx3、二次函数4)1(32xy的顶点坐标是()A.(1,4)B.(-1,4)C.(-1,-4)D(1,-4)4、已知⊙O的直径AB=6cm,则圆上任意一点到圆心的距离是()A.2cmB.3cmC.6cmD.无法确定5、点M(1,-2)关于原点对称的点的坐标是()A.(-1,-2)B.(1,2)C.(-1,2)D.(-2,1)6、在二次函数122xxy的图象中,若y随力的增大而增大,则x的取值范围是()A.x<1B.x>1C.x<-1D.x>-17、用配方法解方程x2-2x-5=0时原方程变形为()A.(x+1)2=6B.(x+2)2=9C.(x-1)2=6D.(x-2)2=98、如图,AB是⊙O的直径,CD⊥AB,垂足为M,则下列结论不成立的是()A.CM=DMB.CB=DBC∠ACD=∠ADCD.OM=MD9、在同一直角坐标系中,函数mmxy和y=-mx2+2x+2,(m是常数,且m≠0)的图象可能是()10、二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论abc<0b+2a=0a+b+c<0b2-4ac>0方程a02cbxx的两根分别是-1,3,其中正确的是()A.1个B.2个C.3个D.4个二、填空题(每题3分,共18分)11、一元二次方程022xx的解为21,xx,则21.xx=_____________,21xx_____________⌒⌒⌒12、将抛物线221xy先向上平移2个单位,再向右平移1个单位后,得到的抛物线解析式是____________13、如图,在Rt△ABC中,∠C=900,∠ABC=600,BC=3cm,BO是∠ABC的平分线交AC于点O,以点O为旋转中心将这个几何图形旋转1800,点B落在B’处,那么点B’与B的距离为___________。14、如图在⊙O中,若∠AOB=1200,弦AB=32则⊙O的半径是___________。15、腾五中要组织一次篮球联赛,赛制为单循环形式,每两队之间都要比赛一场,计划安排15场比赛,则参加比赛的球队大约有_________队。16、若函数y=mx2+2x+1的图象与x轴只有一个公共点,则m的值是___________。三、解答题(共52分)17、解下列方程(每小题3分,共6分)(1)x2+3x-2=0(2)2x(x+4)=4x+1618、(8分)在正方形网格中建立如图所示的平面直角坐标系,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题。(1)画出△ABC关于x轴对称的△A1B1C1。(2)画出△ABC关于原点对称的△A2B2C2。(3)将△ABC绕点B逆时针旋转900,画出旋转后的A3BC3。(4)求△A1A2A3的面积。19、已知关于x的方程0)12()2(2mxmx。(1)求证:方程恒有两个不相等的实数根。(2)若此方程的一个根为1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。20、如图,在⊙O中,OM⊥AB于M,ON⊥CD于N,且OM=ON,求证AB=CD。21、为落实“两免一补”政策,腾冲县2013年投入教育经费2500万元,预计2015年投入教育经费3600万元,已知2013年到2015年的教育经费投入以相同的百分率逐年增长。(1)求每年的平均增长率。(2)按该平均增长率请你帮计算一下2016年腾冲县投入的教育经费为多少万元?22、某商场要经营一种新上市的文具,进价为20元/件。试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售数量就减少10件。(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)求销售单价为多少元时,该文具每天的销售利润最大;⌒⌒23.如图,已知直线33xy分别交x轴、y轴于A、B两点,抛物线cbxxy2经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合)(1)求抛物线的解析式;(2)求△ABC的面积;(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标。座位号:云南省腾冲县第六中学2014年11份月考试题初三数学答题卡一、填空题(每题3分,共30分)题号12345678910答案二、填空题(每题3分,共18分)11、__________________________12、_______________13、___________14、___________15、______________...