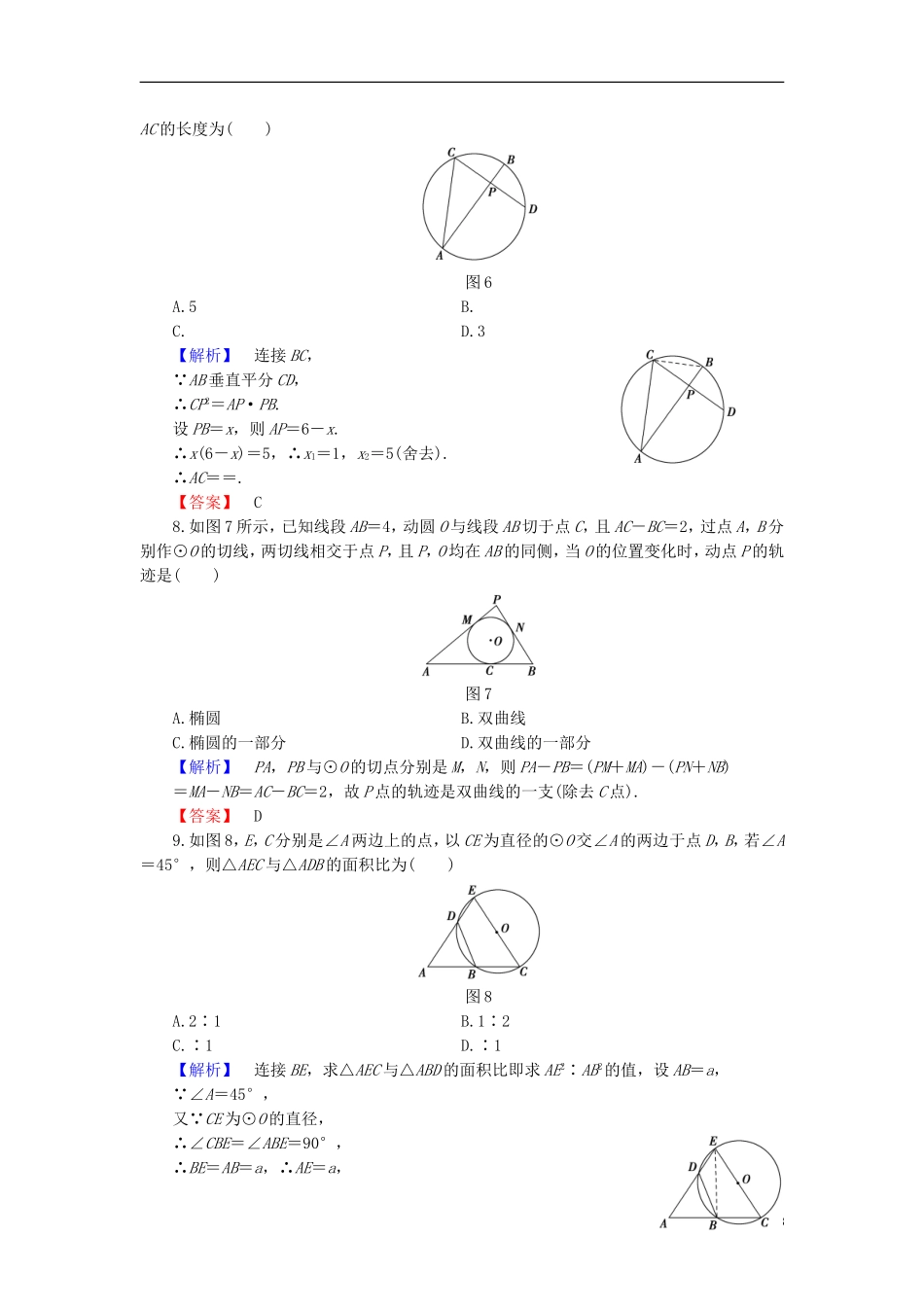
模块综合测评(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图1,已知BN∥AM,ND∥MC,那么有()图1A.=B.=C.=D.以上答案都不对【解析】 BN∥AM,∴=,又 ND∥MC,∴=,∴=.【答案】B2.如图2,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为()图2A.米B.1米C.米D.米【解析】=,得h=(米).【答案】C3.如图3,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF等于()图3A.40°B.55°C.65°D.70°【解析】 ∠B=50°,∠C=60°,∴∠A=70°,∴∠EOF=110°,∴∠EDF=55°.【答案】B4.已知:如图4,▱ABCD中,EF∥AC交AD,DC于E,F,AD,BF的延长线交于M,则下列等式成立的是()1图4A.AD2=AE·AMB.AD2=CF·DCC.AD2=BC·ABD.AD2=AE·ED【解析】 在▱ABCD中,∴AD∥BC,AB∥DC. DF∥AB,∴=.∴DM∥BC,∴=. EF∥AC,∴=.∴=,∴AD2=AE·AM.【答案】A5.如图5,PT是⊙O的切线,且PT的长为4,PBC是⊙O的一条割线,EF和BC是⊙O内两条相交于M的弦,已知PB=2,BM∶MC=2∶1,EM∶MF=2∶1,则MC,MF的长分别为()图5A.2,2B.2,4C.2,1D.1,2【解析】 PT2=PB·PC,设CM=x,则MB=2x,∴16=2(2+3x),∴x=2.设EM=2t,MF=t,又 BM·MC=EM·MF,∴2t·t=2x2=8,∴t=2,∴MC=x=2,MF=t=2.【答案】A6.已知圆柱的底面半径为2,平面π与圆柱斜截口图形的离心率为,则椭圆的长半轴长是()A.2B.C.4D.【解析】由题意知,短半轴b=2,==,∴=,解得a=.故选B.【答案】B7.如图6,AB、CD是圆O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2,则线段2AC的长度为()图6A.5B.C.D.3【解析】连接BC, AB垂直平分CD,∴CP2=AP·PB.设PB=x,则AP=6-x.∴x(6-x)=5,∴x1=1,x2=5(舍去).∴AC==.【答案】C8.如图7所示,已知线段AB=4,动圆O与线段AB切于点C,且AC-BC=2,过点A,B分别作⊙O的切线,两切线相交于点P,且P,O均在AB的同侧,当O的位置变化时,动点P的轨迹是()图7A.椭圆B.双曲线C.椭圆的一部分D.双曲线的一部分【解析】PA,PB与⊙O的切点分别是M,N,则PA-PB=(PM+MA)-(PN+NB)=MA-NB=AC-BC=2,故P点的轨迹是双曲线的一支(除去C点).【答案】D9.如图8,E,C分别是∠A两边上的点,以CE为直径的⊙O交∠A的两边于点D,B,若∠A=45°,则△AEC与△ADB的面积比为()图8A.2∶1B.1∶2C.∶1D.∶1【解析】连接BE,求△AEC与△ABD的面积比即求AE2∶AB2的值,设AB=a, ∠A=45°,又 CE为⊙O的直径,∴∠CBE=∠ABE=90°,∴BE=AB=a,∴AE=a,3∴AE2∶AB2=2a2∶a2,即AE2∶AB2=2∶1,∴S△AEC∶S△ADB=2∶1.【答案】A10.如图9,△ABC的底边BC=a,高AD=h,矩形EFGH内接于△ABC,其中E,F分别在边AC,AB上,G,H都在BC上,且EF=2FG,则矩形EFGH的周长是()图9A.B.C.D.【解析】设FG=x,因为EF=2FG,所以EF=2x.因为EF∥BC,所以△AFE∽△ABC.又AD⊥BC,设AD交EF于M,则AM⊥EF.所以=,即=.所以=.解之,得x=.所以矩形EFGH的周长为6x=.【答案】B11.如图10,正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为()图10A.πB.C.D.【解析】(图略)设△ABC的中心是E,球心O到平面ABC的距离为1,即OE=1,故AE===,从而ED=,所以OD==,故面积最小的截面圆半径为r==,所以截面面积的最小值为S=πr2=π.【答案】B12.(广东高考)若实数k满足0