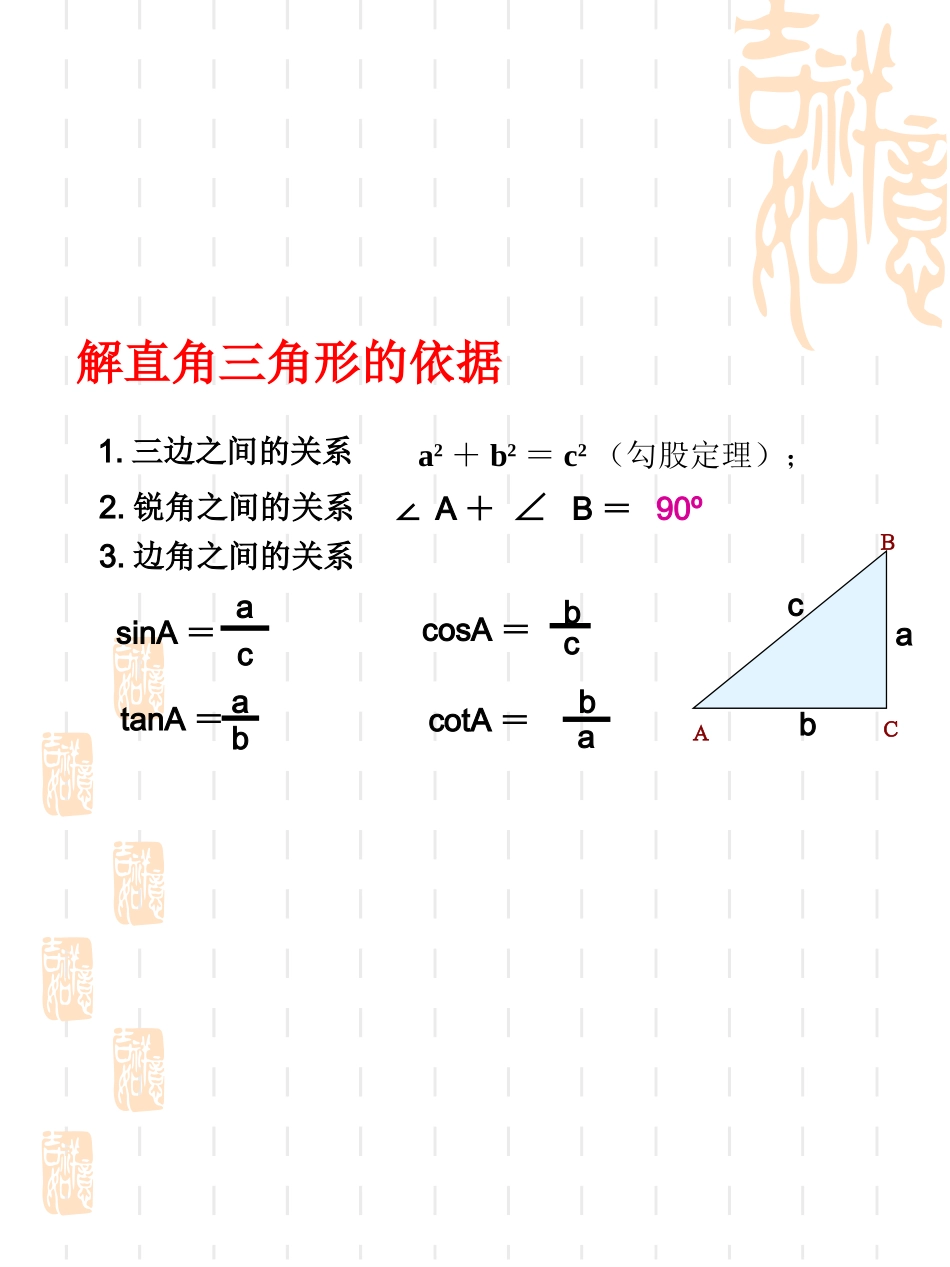
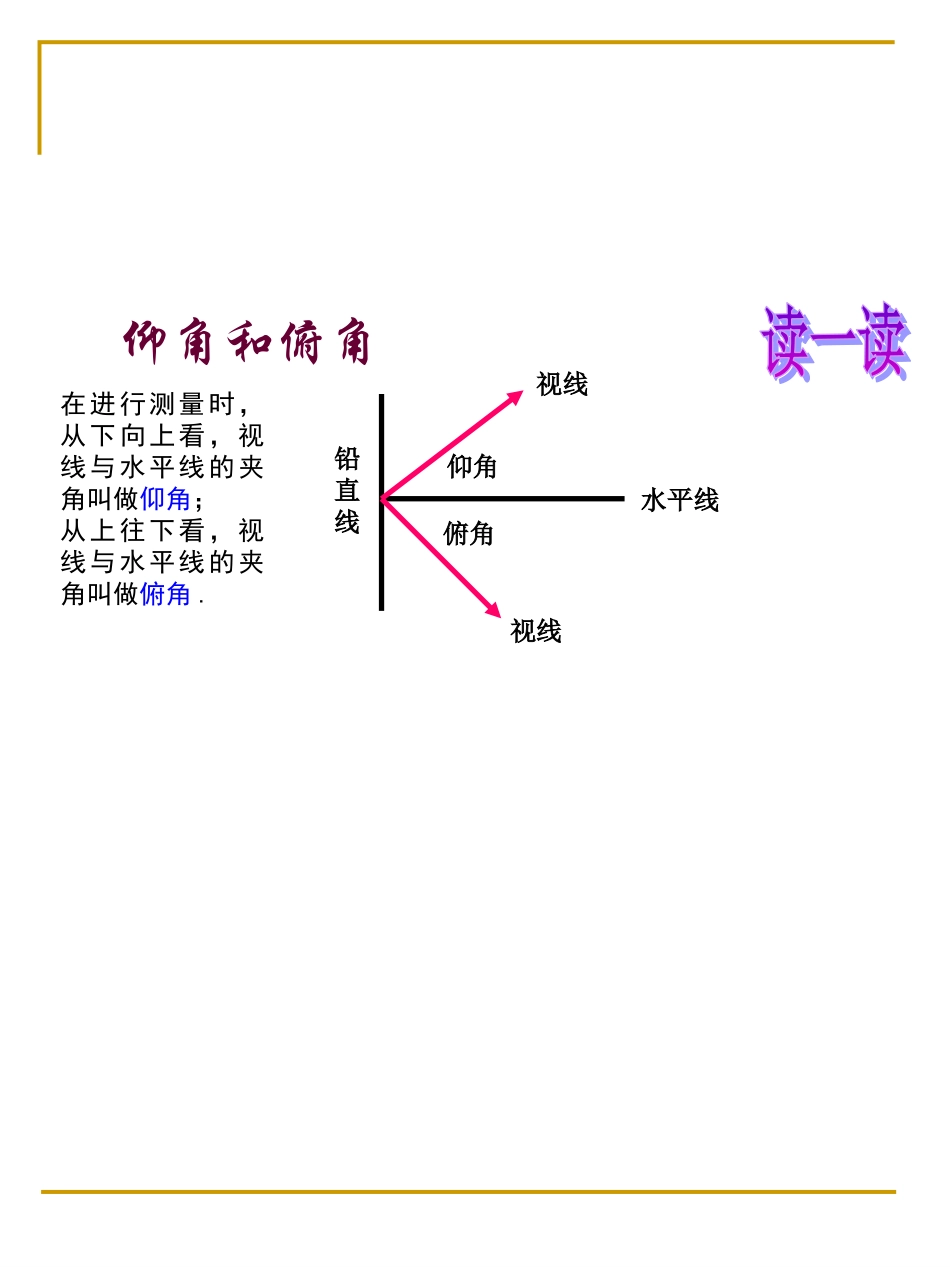
1.三边之间的关系a2+b2=c2(勾股定理);2.锐角之间的关系∠A+∠B=90º3.边角之间的关系tanA=absinA=accotA=ba解直角三角形的依据cosA=bcACBabc仰角和俯角铅直线水平线视线视线仰角俯角在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.例3解在RtBDE△中,BE=DE×tana=AC×tana=22.7×tan22°≈22.7×0.4040≈9.17,所以AB=BE+AE=BE+CD=9.17+1.20≈10.4(米).答:电线杆的高度约为10.4米.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)如图,河对岸有铁塔AB,在C处测得塔顶的仰角为300,向塔前进14米至D处,测得A的仰角为450,1.若设AB为x,求BC(用x的代数式表示),2.求此铁塔AB的高.问题1CADB3004502.设AB为x,在Rt△ABD中,∠ADB=45°,则AB=BD=x,BC=BD+CD=x+14,在Rt△ABC中,∠ACB=30°,解:1.因ABBC,ADB=45°,⊥∠则BD=AB=x,则BC=CD+BD=14+x.1.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离.(精确到1米)练习αABC2.两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=25゜,测得其底部C的俯角a=50゜,求两座建筑物AB及CD的高.(精确到0.1米)(第2题)1.课本第98页习题第3题2.102页10题