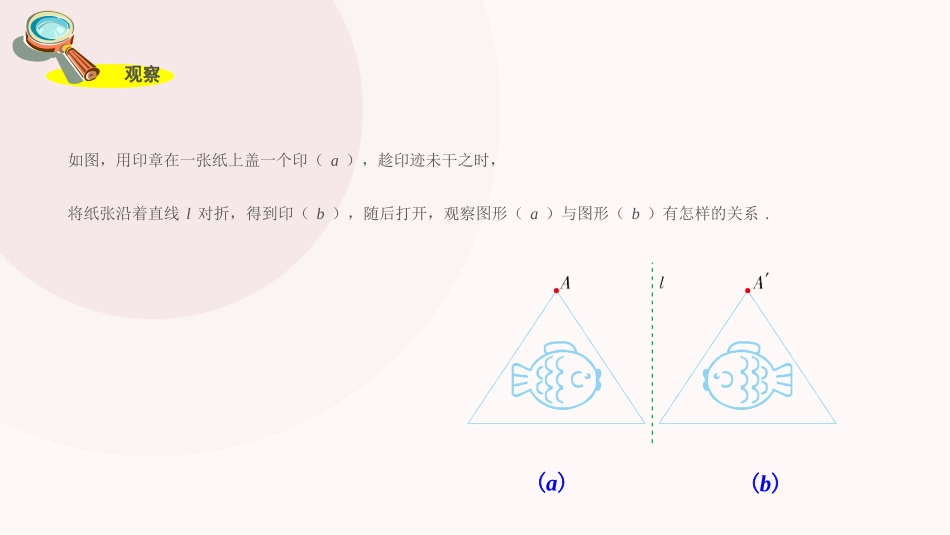
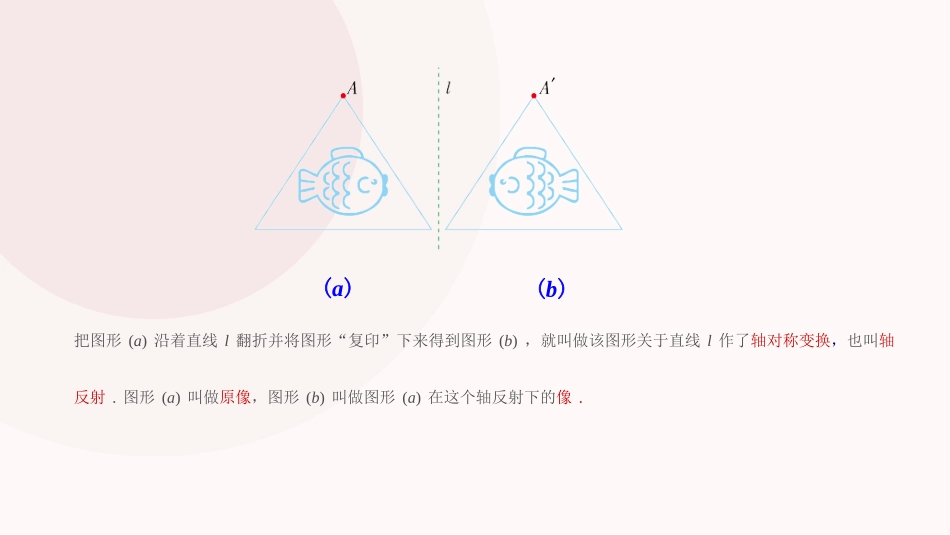
5.1.2轴对称变换5.1轴对称第五章轴对称与旋转如图,用印章在一张纸上盖一个印(a),趁印迹未干之时,将纸张沿着直线l对折,得到印(b),随后打开,观察图形(a)与图形(b)有怎样的关系.(a)(b)观察把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.图形(a)叫做原像,图形(b)叫做图形(a)在这个轴反射下的像.(a)(b)如果一个图形关于某一条直线做轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.这条直线叫做对称轴.原像与像中能互相重合的两个点,其中一点叫做另一个点关于这条直线的对应点.(a)(b)上图中,对称轴l两边的图形(a)与(b)的形状和大小发生变化了吗?轴对称变换具有下述性质:例如:长度、角度和面积等都不改变.上图中,两图形的形状和大小均没有发生改变.轴对称变换不改变图形的形状与大小.讨论(a)(b)探究在图中,三角形ABC和三角形关于直线l成轴对称,点P和P′是对应点,线段PP′交直线l于点D。那么线段PP′与对称轴l有什么关系呢?ABC因为三角形ABC和三角形A′B′C′关于直线l成轴对称,将图沿直线l折叠,则点P与_____重合,所以PD与_______,∠1与_______也互相重合,故有PD=_____,∠1=∠___=____°,因此,l_____PP′,且___________PP′,即直线l__________线段PP′。结论成轴对称的两个图形中,对应点的连线被对称轴垂直平分。成轴对称的两个图形中,对应点的连线被对称轴垂直平分。轴对称具有下述性质:从图中可以看出,如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。说一说如何做一个图形关于一条直线的对称图形?【例1】如图,已知直线l及直线外一点P,求作点P',使它与点P关于直线l对称.作法:1.过点P作PQ⊥l,交l于点O..POP'lQ2.在直线PQ上,截取OP'=OP.则点P'即为所求作的点.如左图,已知线段AB和直线l,作出与线段AB关于直线l对称的图形.lABA'B')作法:1.过点A作直线l的垂线,垂足为点O,在垂线上截取OA'=OA,点A'就是点A关于直线l的对应点.2.类似地,分别作出点B,C关于直线l的对应点B',C'.3.连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.【例2】如图,已知三角形ABC和直线l,作出与三角形ABC关于直线l对称的图形.分析:要作三角形ABC关于直线l的对称图形,只要作出三角形的顶点A,B,C关于直线l的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC关于直线l对称的图形.lACA'B'C'OB2.下列三个图案分别成轴对称吗?如果是,画出它们的对称轴,并标出一对对应点。练习通过本节课,你有什么收获?你还存在哪些疑问,和同伴交流。我思我进步