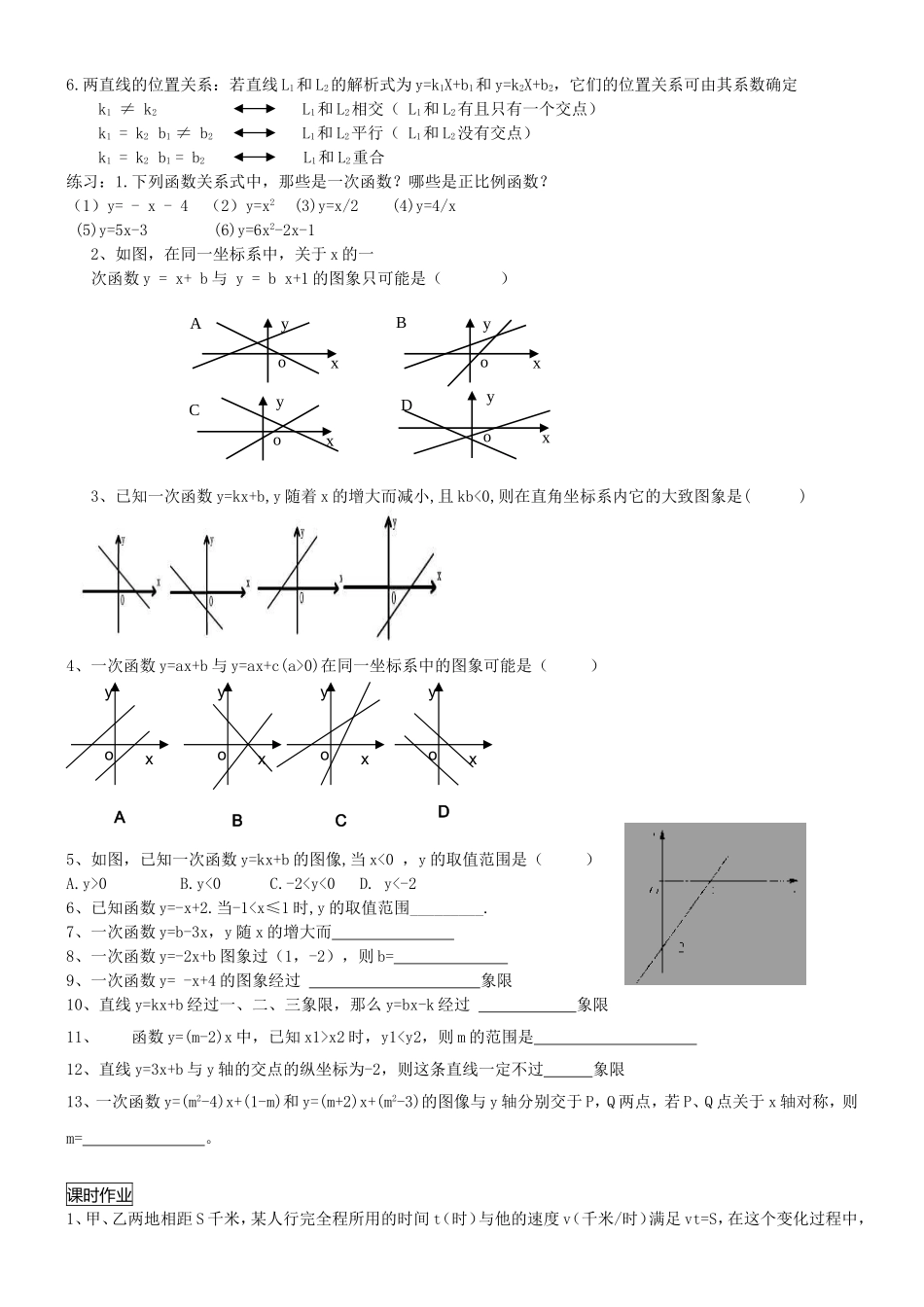
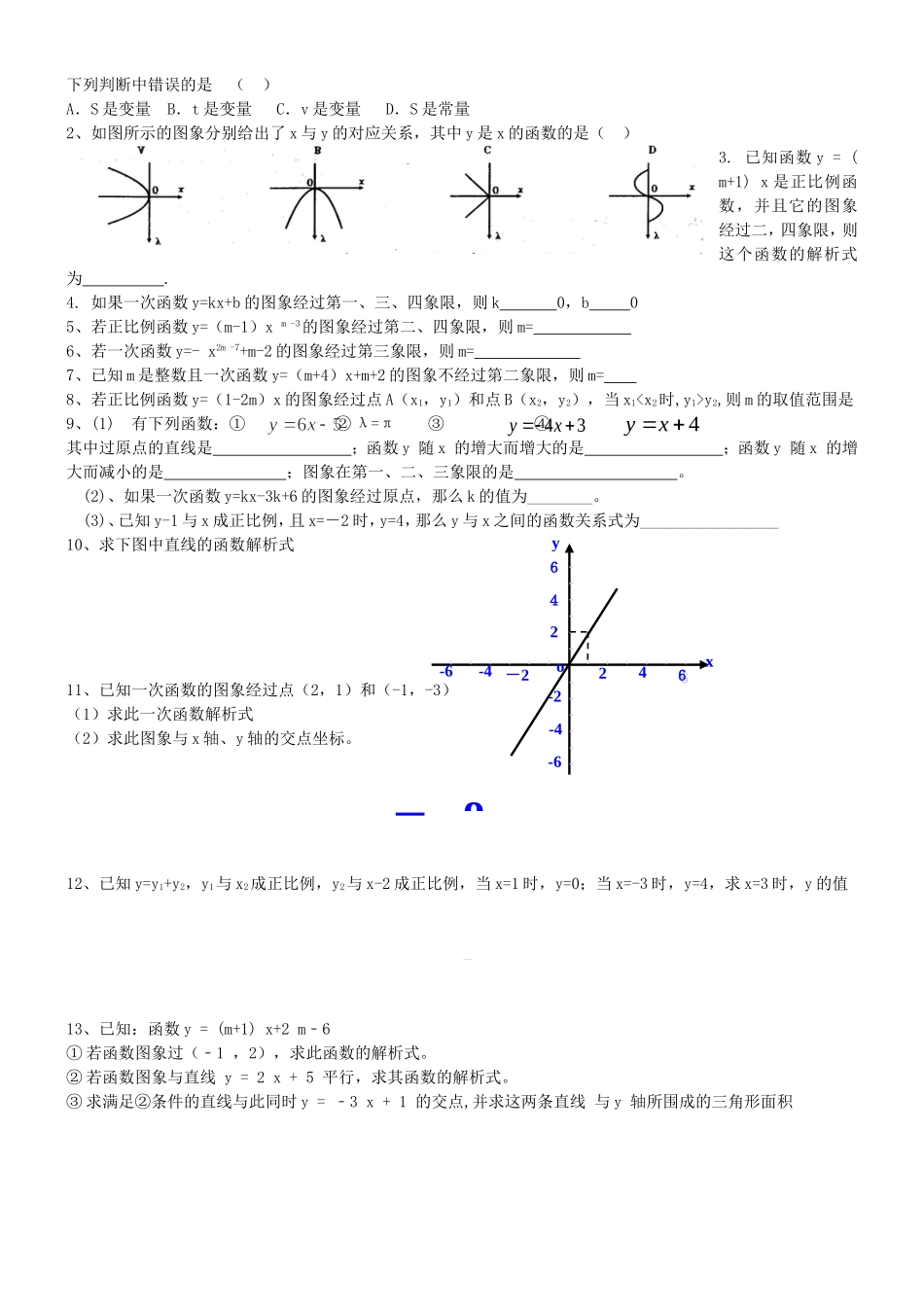
一次函数复习课导学案(1)学习目标:1、知道什么是函数,并能判断某变化过程中两个变量之间的关系是否函数关系;2、知道什么是一次函数、正比例函数,并能判断一个函数是不是一次函数和正比例函数;3、会运用一次函数图像及性质解决简单的问题;4、会用待定系数法确定一次函数的解析式。基本知识点突破:1、(1)函数的概念:一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就唯一确定了一个y值,那么就是_____的函数;(2).函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的,那么坐标平面内由这些点组成的图形,就是这个函数的图象。(3)、描点法画图象的步骤:(4).函数的三种表示方法:(5)、自变量的取值范围:(1)分式类:分母不为0,(2)根式类:开偶次方的被开方数大于等于0,(3)整式类:所有实数。(4)实际类:使实际问题有意义。练习:1、求下列函数中自变量x的取值范围(1)y=x(x+3);(2)y=(3)y=(4)y=2、下列四组函数中,表示同一函数的是()A、y=x与y=B、y=x与y=()2C、y=x与y=x2/xD、y=x与y=2、一次函数的概念:若两个变量x,y间的函数关系式可以表示成的形式,则称是的一次函数,为自变量,为因变量。特别地,时,称。正比例函数是_____________的特殊形式,因此正比例函数都是_______,而一次函数不一定都是_________.3、判断一个函数是不是一次函数的条件:(1)、的个数;(2)、自变量的和;(3)、分母中是否含有4、一次函数图像、性质及其解析式的确定:函数类型k、b的取值范围图像增减性经过特殊点函数解析式的确定(基本思路)y=kx+b(k≠0,b为常数)k﹥0b﹥0与x轴的交点坐标是(,),与y轴的交点坐标是(,)1、设函数解析式为2、代入已知两点的坐标或者x,y的两组对应值,得到3、解4、写出函数解析式b﹤0k﹤0b﹥0b﹤0y=kx(k≠0)k﹥0正比例函数的图像都经过(,)1、设函数解析式为2、代入已知一点的坐标或者x,y的一组对应值,得到3、解4、写出函数解析式k﹤05、一次函数y=kx+b的图象是一条直线,其中k决定直线增减性,b决定直线与y轴的交点位置.k和b决定了直线所在的象限.843x12x532xx3x36.两直线的位置关系:若直线L1和L2的解析式为y=k1X+b1和y=k2X+b2,它们的位置关系可由其系数确定k1≠k2L1和L2相交(L1和L2有且只有一个交点)k1=k2b1≠b2L1和L2平行(L1和L2没有交点)k1=k2b1=b2L1和L2重合练习:1.下列函数关系式中,那些是一次函数?哪些是正比例函数?(1)y=-x-4(2)y=x2(3)y=x/2(4)y=4/x(5)y=5x-3(6)y=6x2-2x-12、如图,在同一坐标系中,关于x的一次函数y=x+b与y=bx+1的图象只可能是()3、已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是()4、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是()5、如图,已知一次函数y=kx+b的图像,当x<0,y的取值范围是()A.y>0B.y<0C.-2x2时,y1