1.2二次函数的图象VIP免费

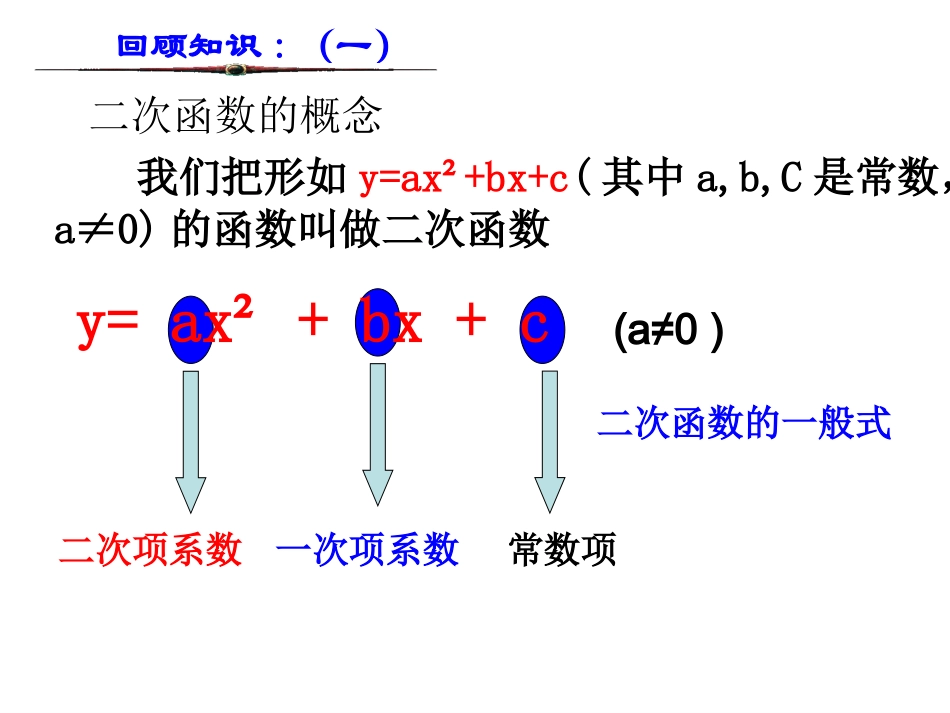
1.2二次函数的图像(1)我们把形如y=ax²+bx+c(其中a,b,C是常数，a≠0)的函数叫做二次函数y=ax²+bx+c二次项系数一次项系数常数项二次函数的一般式(a≠0)回顾知识:（一）二次函数的概念回顾知识:（二）一、正比例函数y=kx（k≠0）的图象是什么。二、一次函数y=kx+b（k≠0）的图象又是什么。一条经过原点的直线。是一条直线。三、反比例函数（k≠0）的图象又是什么。xky是双曲线那么二次函数y=ax²+bx+c（a≠0）的图象又是什么呢？。画出下列函数的图象。22-)2()1(xyxyxy=x2y=-x2..................0-2-1.5-1-0.511.50.52函数图象画法列表描点连线00.2512.2540.2512.254描点法用光滑曲线连结时要自左向右顺次连结0-0.25-1-2.25-4-0.25-1-2.25-4注意：列表时自变量取值要均匀和对称。2xy2xy抛物线抛物线例1在同一直角坐标系中，画出函数的图象．222,21xyxy解：分别填表，再画出它们的图象，如图x···－4－3－2－101234·········x···－2－1.5－1－0.500.511.52·········212yx22yx84.520.5084.520.584.520.5084.520.5－222464－48212yx22yx2yx函数的图象与函数y=x2的图象相比，有什么共同点和不同点？222,21xyxy－222464－48212yx22yx2yx相同点：开口都向上，顶点是原点而且是抛物线的最低点，对称轴是y轴不同点：a要越大，抛物线的开口越小．你画出的图象与图中相同吗？探究画出函数的图象，并考虑这些抛物线有什么共同点和不同点．2222,21,xyxyxyx···－4－3－2－101234·········x···－2－1.5－1－0.500.511.52·········212yx22yx－8－4.5－2－0.50－8－4.5－2－0.5－8－4.5－2－0.50－8－4.5－2－0.5－22－2－4－64－4－8212yx22yx2yx对比抛物线，y=x2和y=－x2.它们关于x轴对称吗？一般地，抛物线y=ax2和y=－ax2呢？1、抛物线y=ax2的顶点是原点，对称轴是y轴。2、当a>0时，抛物线的开口向上，顶点是抛物线上的最低点，在对称轴的左侧，y随着x的增大而减小；在对称轴右侧，y随着x的增大而增大。当x=0时函数y的值最小；当a<0时，抛物线的开口向下，顶点是抛物线上的最高点，在对称轴的左侧，y随着x的增大而增大；在对称轴右侧，y随着x的增大而减小。当x=0时函数y的值最大；二次函数y=ax2的性质二次函数y=ax2的性质2xy2xy课堂小结形如（a、b、c是常数，a≠0）的函数叫做x的二次函数，a叫做二次函数的系数，b叫做一次项的系数，c叫作常数项。2yaxbxc=++1.二次函数：2、抛物线：二次函数的图象都是抛物线。一般地，抛物线y=ax2的对称轴是____轴，顶点是_______.当a>0时，抛物线的开口向__，顶点是抛物线的________，a越大，抛物线的开口越___;当a<0时，抛物线的开口向____，顶点是抛物线的最____点，a越大，抛物线的开口越____.y原点最低点上小下高大3、抛物线y=ax2的图象：4、抛物线y=ax2的图象中a决定开口方向和形状。a相同开口方向相同、形状相同，|a|越大，开口越小。